Sequel of previous post : Static Solutions

In this series of posts about the history of relativistic cosmology, I  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaître, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaître, although his papers remain mostly  unquoted.

The Friedmann’s pioneering work

In an article which appeared in 1922, entitled On the Curvature of Space (see Luminet 2004 for reference and translation), the Russian physicist Alexander Friedmann took the step which Einstein had balked at : he abandoned the theory of a static universe, proposing a “dynamic” alternative in which space varied with time. As he stated in the introduction, “the goal of this notice is the proof of the possibility of a universe whose spatial curvature is constant with respect to the three spatial coordinates and depend on time, e.g. on the fourth coordinate.“

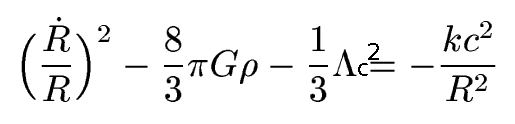
Thus he assumed a positively curved space (hypersphere), a time variable matter density and a vanishing cosmological contant. He obtained his famous “closed universe model”, with a dynamics of expansion – contraction. Continue reading →