Sequel of previous post :  From Myth to Science

In this series of posts about the history of relativistic cosmology, I  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaître, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaître, although his papers remain mostly  unquoted.

The History of Relativistic Cosmology can be divided into 6 periods :

– the initial one (1917-1927), during which the first relativistic universe models were derived in the absence of any cosmological clue.

– a period of development (1927-1945), during which the cosmological redshifts were discovered and interpreted in the framework of dynamical Friedmann-Lemaître solutions, whose geometrical and mathematical aspects were investigated in more details.

– a period of consolidation (1945-1965), during which primordial nucleosynthesis of light elements and fossil radiation were predicted.

– a period of acceptation (1965-1980), during which the big bang theory triumphed over the « rival » steady state theory.

– a period of enlargement (1980-1998), when high energy physics and quantum effects were introduced for describing the early universe.

– the present period of high precision experimental cosmology, where the fundamental cosmological parameters are now measured with a precision of a few %, and new problematics arise (nature of the dark energy, topology of the universe, new cosmologies in quantum gravity theories, etc.)

Let us follow chonologically the rather hectic evolution of the ideas in the field.

The beginnings of Relativistic Cosmology : static solutions.

In 1915, Einstein and Hilbert provided the correct field equations for a relativistic theory of gravitation. This new theory, coined as « General Relativity », proposed a new framework for understanding the universe. Einstein argued that gravity was not a force but an effect of the curvature of space-time caused by the distribution of mass and energy. The theory allows scientists to overhaul cosmological theory : the universe, until then a relatively vague concept, acquires a new consistency and becomes a physical entity defined by its space-time structure and its composition of matter, light, radiation, in fact all kinds of energy. Space-time is endowed with a rich structure, expressed geometrically in terms of curvature and topology, and physically in terms of its matter and energy contents.

Albert Einstein

David Hilbert

Cosmological solutions of Einstein’s equations are obtained by assuming homogeneity and isotropy in the matter-energy distribution. This implies that space curvature is on the average constant (i.e. it does not vary from point to point, although it may change with time).

The first exact solution was obtained in 1917 by Einstein himself, who quite naturally wished to use his brand new theory of general relativity to describe the structure of the Universe as a whole (for Germanophone readers, the original article can be read here). He assumed that space has a positive curvature, i.e. the geometry of the Riemannian hypersphere, and searched for a static solution, i.e. in which the average matter density is constant over time, as well as the radius of the hyperspherical space. Einstein expected that general relativity would support this view. However this was not the case. The model universe that he initially calculated did not have a constant radius of curvature : the inexorable force of gravity, acting on each celestial body, had a tendency to make it collapse. For Einstein, the only remedy was to add an ad hoc but mathematically coherent term to his original equations. This addition corresponds to some sort of « antigravity », which acts like a repulsive force that only makes itself felt at the cosmic scale. Thanks to this mathematical trick, Einstein’s model remained as permanent and invariable as the apparent Universe. The new term, called the « cosmological constant », has to keep exactly the same value in space and time. Formally, it can take any value whatsoever a priori, but Einstein fitted it to a specific value l_E in order to constrain the radius R_E of the hypersphere and the matter density r to remain constant over time. He thus derived the relation l_E = 1/R_E² .

 

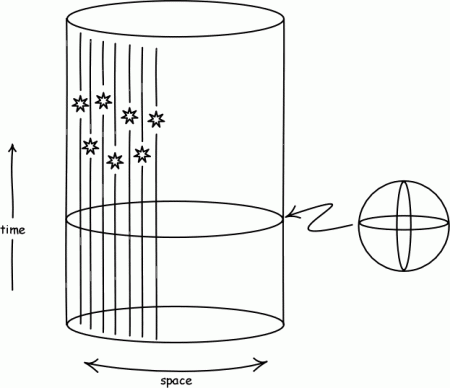
For Einstein, the fact that space had to be static was a natural assumption since at this time, no astronomical observation indicated that stars have large velocities. In fact, his main motivation was to get a finite space (although without a boundary) and try to fit his solution with Mach’s ideas about the origin of inertia : «  I must not fail to mention that a theoretical argument can be adduced in favour of the hypothesis of a finite universe. The general theory of relativity teaches that the inertia of a given body is greater as there are more ponderable masses in proximity to it; thus it seems very natural to reduce the total effect of inertia of a body to action and reaction between it and the other bodies in the universe, as indeed, ever since Newton’s time, gravity has been completely reduced to action and reaction between bodies. From the equations of the general theory of relativity it can be deduced that this total reduction of inertia to reciprocal action between masses – as required by E. Mach, for example – is possible only if the universe is spatially finite. »[1]

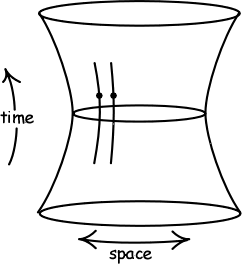
In the same year, 1917, the Dutch astrophysicist Willem de Sitter derived another model for a static relativistic universe, which was very different from that of Einstein. He assumed that space is positively curved (in factthe projective hypersphere, also called elliptic space, where the antipodal points of the ordinary hypersphere are identified), and empty (in other words, the matter density is zero). As a counterpart, in the absence of matter and therefore of gravity, only a cosmological constant can determine the curvature of space, through the relation l = 3/R². A strange consequence was that, although the hyperspherical space was assumed to be static (i.e. R = const), the spatial separation between any two test particles (stars, galaxies) had to increase with time. This meant that the cosmological constant has a particular influence on the structure of space : it generates « motion without matter ». For Einstein, de Sitter’s solution reduced to a simple mathematical curiosity, since the real Universe indeed has a mass.

[1] A. Einstein, Geometry and Experience, Address to the Prussian Academy of Sciences in Berlin on January 27^th, 1921.

The Rise of Big Bang Models (part 3) will follow.