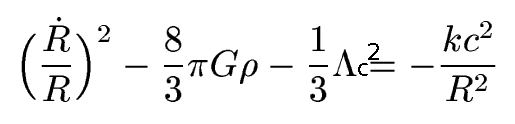Tag Archives: Big bang

Astronomy, History of Science & Epistemology, My books & articles

Alexander Friedmann and the Big Bang : A scientific revolution

Leave a comment

The following is an excerpt from Chapter 4 and 5 of the book  The Big Bang Revolutionaries: The Untold Story of Three Scientists Who Reenchanted Cosmology, by Jean-Pierre Luminet.

The book has received rave reviews including from three Nobel Prize winners.

****

In 1922, Alexander Friedmann took the step that Albert Einstein had not been ready to take: if one abandons the hypothesis of a static universe, the relativistic cosmological problem comprises an infinite number of solutions in which the metric varies as a function of time. Friedmann wrote:

Thus begins this founding notice of non-static cosmology. Received on June 29, 1922, by the German journal Zeitschrift für Physik, it was published shortly afterwards.

Ahead of Its Time

Friedmann’s article was ahead of its time, as one can also see from the fact that anybody studying modern cosmology can immediately recognize its main equations. While the formulations of the various metrics (de Sitter’s as well as Friedmann’s) would later change to the unified form of Howard Robertson and Arthur Walker, the differential equations that govern the time development of a space of constant positive curvature have not changed one iota.

With his 1922 article, Friedmann introduced a scientific revolution of the same magnitude as the Copernican revolution. In pre-Copernican cosmology, space was centered on a very particular place, the Earth. In pre-Friedmannian cosmology, the universe was static, in the sense of not evolving. Friedmannian cosmology introduces the historicity of the universe as space-time, as well as the idea of a beginning.

His second major cosmological article appeared in 1924. In 1925, he was appointed director of the Leningrad Geophysical Institute. In the summer of 1925, in the company of the aviator P. F. Fedosenko, he beat the altitude record in a stratospheric balloon, rising to 7,400 meters.

Friedmann died suddenly in Leningrad on September 16, 1925, from typhoid fever, at the age of thirty-seven. In 1931, he was posthumously awarded the Lenin Prize for his outstanding scientific work.

In Search of a Lost Tomb

Friedmann is buried in his hometown. An instructive anecdote is worth telling. The location of the Russian scientist’s grave was quickly forgotten, especially since the Stalinist regime that followed was hardly inclined to perpetuate the memory of this renowned “creationist” scientist. In 1988, the Alexander Friedmann Laboratory of the University of St. Petersburg (then called Leningrad State University) decided to organize the first “A. Friedmann International Seminar in Cosmology” to honor the centenary of the scientist’s birth. The director of the Friedmann Institute, my friend Andrey Grib, had the idea of a search for Friedmann’s tomb, planning a small commemorative ceremony in which admirers from various countries would participate. A venerable professor at the Institute of Physics and Technology in St. Petersburg and a former PhD student of Friedmann, Georgy Grinberg, remembered having attended the funeral of the scientist at the Smolenskoye Cemetery, and that the cosmologist’s grave was close to that of the great mathematician Leonhard Euler.

Grib therefore asked one of his students, Mihail Rosenberg, to go to the cemetery to locate the tomb — even hinting that this task would be recognized as part of his thesis work. When Rosenberg went to the cemetery and asked to consult the register of all the people buried here, the authorities replied that they had no information from prior to World War II. Rosenberg then asked to see the tomb of Leonhard Euler. After the war, he was told, Euler’s remains were transferred to another cemetery. There remained at least the old location, which the authorities indicated to him. Rosenberg explored the surroundings but found no evidence of Friedmann’s presence. He then began to quarrel with the authorities: How can the records have disappeared? At this point, an attendant approached and inquired about the dispute. The director of the cemetery replied that the student was looking for a certain “Friedmann.” “Which Friedmann,” asked the employee, “the one who discovered the non-static cosmological solution to Einstein’s equations?”

“Yes, yes,” exclaimed the student.

“Well, come with me, I’ll show you!”

This is how the cosmologist’s grave was discovered. The cemetery employee was none other than a former physicist who’d had to leave his research institute for lack of funds.

****

Jean-Pierre Luminet, a French astrophysicist specializing in black holes and cosmology, is emeritus research director at the French National Centre for Scientific Research. He is a member of the Laboratoire d’Astrophysique de Marseille (LAM) and Laboratoire Univers et Théories (LUTH) of the Paris-Meudon Observatory. Luminet has been awarded several prizes. These include the Georges Lemaître Prize (1999) for his work in cosmology, the UNESCO Kalinga Prize (2021), and the Einstein medal for the Popularization of Science (2021). He has published more than twenty science books, eight historical novels, and eight poetry collections. The asteroid 5523 Luminet was named in his honor.

History of Science & Epistemology, My books & articles, Sciences

The Big Bang Revolutionaries

Leave a comment

The Big Bang Revolutionaries  : The Untold Story of Three Scientists Who Reenchanted Cosmology

by Jean-Pierre Luminet

Many widely read scientific writers of our day mistakenly attribute the concepts of the expanding universe and the Big Bang to Edwin Hubble and Albert Einstein. Hubble did provide evidence of an expanding universe, but he neither discovered such evidence nor accepted the radical idea that space itself was expanding. As for Einstein, he held out against the idea of an expanding universe for more than a decade, and ceased working in the field as soon as he had to amend his view. The real heroes of the Big Bang revolution are the Russian Alexander Friedmann and Belgian priest Georges Lemaître. That they are virtually unknown to the general public is one thing. That their contribution is underestimated by astrophysicists and cosmologists is another, for the concepts they promulgated are among the most remarkable achievements of twentieth-century science. The Big Bang Revolutionaries amends the record, telling the remarkable story of how these two men, joined by the mischievous George Gamow and in the face of conventional scientific wisdom, offered a compelling view of a singular creation of the universe in what Lemaître termed a “primeval atom.”

Publisher : Discovery Institute Press
Published : April 23, 2024
ISBN : 978-1-63712-040-8
Pages : 254
Retail Price : $18.95

Jean-Pierre Luminet, a French astrophysicist specializing in black holes and cosmology, is emeritus research director at the French National Centre for Scientific Research. He is a member of the Laboratoire d’Astrophysique de Marseille (LAM) and Laboratoire Univers et Théories (LUTH) of the Paris-Meudon Observatory. Luminet has been awarded several prizes. These include the Georges Lemaître Prize (1999) for his work in cosmology, the UNESCO Kalinga Prize (2021), and the Einstein medal for the Popularization of Science (2021). He has published more than twenty science books, eight historical novels, and eight poetry collections. The asteroid 5523 Luminet was named in his honor.

Advance Praise

This excellent and well-illustrated book convincingly puts into a clear focus the key original contributions of Friedmann and Lemaître in the early twentieth-century revolution in our understanding of the large-scale physical universe.

Roger Penrose, Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute of the University of Oxford, Emeritus Fellow of Wadham College at Oxford, fellow of the Royal Society, and recipient of the Wolf Prize (1988) and the Nobel Prize in Physics (2020)

The author brings together many aspects of thinking about the large-scale nature of our world from the points of view of concepts, theory, observation, and culture. The account starts with Albert Einstein’s thought that a philosophically satisfactory universe has no boundary, a bold conjecture that proved to fit well with Einstein’s new gravity theory and now agrees with the observational evidence. You will find fascinating details of the evolution of ideas, evidence, and the cultural situation between that time and the early steps by which George Gamow’s brilliant intuition took him to the realization that an even better picture of our universe is that it expanded from a hot dense state.

Jim Peebles, the Albert Einstein Professor in Science, emeritus, Princeton University, and recipient of the 2019 Nobel Prize in Physics

It is rare to find an internationally distinguished astrophysicist who is also a searching and meticulous historian. It is rarer still to find such a person who is also a gifted prose stylist. Jean-Pierre Luminet is such a man. The Big Bang Revolutionaries is invaluable reading for anyone fascinated by the history of the big ideas that have shaped and reshaped Western science and civilization, and for anyone who wants a front row seat to witness the all-too-common character of scientific revolution—messy, full of unexpected twists and turns, and not without its casualties. In the present case and as Luminet dramatically shows, the revolution occurred in the face of sustained prejudice from some of the finest minds in physics and astronomy. As for the wider implications of the Big Bang revolution, Luminet leaves those for the reader to contemplate.

Stephen C. Meyer, Director of the Center for Science and Culture and author of Signature in the Cell, named a Book of the Year by the Times (of London) Literary Supplement, Return of the God Hypothesis, and the New York Times bestseller Darwin’s Doubt

The twentieth century represents an exceptional period in the study of the cosmos. But this century will be remembered above all as the one in which physics, for the first time, made it possible to study the universe and its evolution. Jean-Pierre Luminet, an eminent cosmologist, takes the role of historian in this analysis of the emergence of ideas, and pays tribute to the physicists who contributed to this dizzying scientific adventure.

Michael Mayor, Swiss astrophysicist and professor emeritus at the University of Geneva; a recipient of the Viktor Ambartsumian International Prize (2010), the Kyoto Prize (2015), and the Nobel Prize in Physics (2019)

An inspiring overview of the history and physics of our modern view of the universe by the brilliant scientist Jean-Pierre Luminet, who was first to simulate black hole silhouettes. The reader is introduced to the scientific insights that revolutionized the perception of our cosmic roots and future. A fascinating read!

Abraham (Avi) Loeb, Frank B. Baird Jr. Professor of Science and Director of the Institute for Theory & Computation, Harvard University, and director for the Breakthrough Initiatives of the Breakthrough Prize Foundation

This book is a very careful discussion of the work of three less-known key figures who laid the foundations of modern cosmology—Alexander Friedmann, Georges Lemaître, and George Gamow. It does a great service in detailing the contributions that each of them made to the topic. I particularly appreciate the discussion of the pioneering work and personality of Lemaître, who can justly be called the father of scientific cosmology. With its discussion also of cosmic topology, the book is a unique contribution to the history of cosmology.

George Ellis, emeritus distinguished professor, University of Cape Town, co-author with Stephen Hawking of The Large Scale Structure of Space-Time, former president of the International Society on General Relativity and Gravitation, fellow of the Royal Society, recipient of the Templeton Prize and the Georges Lemaître International Prize

The Big Bang Revolutionaries is one terrific book. And one, I might add, of historical importance inasmuch as it restores to their rightful place two fascinating figures whom the standard history of physics in the twentieth century has shamefully neglected. Lucid? Of course it is lucid. Luminet is a fine astrophysicist. Moving? Very much so, not only for what it says about Friedmann and Lemaître, but for what it reveals about the author’s sensitive intelligence on encountering the story of men whose position of prominence was denied them. It is, all in all, a splendid restoration—something very French, I might add, in that it describes men who should have been monarchs reacquiring their thrones.

David Berlinski, Senior Fellow of the Center for Science and Culture, and author of A Tour of the Calculus, The Advent of the Algorithm, Newton’s Gift, The Devil’s Delusion: Atheism and Its Scientific Pretensions, and Science After Babel

Finally a book that brings the credit of the great cosmological revolution of the twentieth century to where it is properly due: the Russian Alexander Friedmann and the Belgian priest Georges Lemaître.

Carlo Rovelli, founder of the quantum gravity group of the Centre de Physique Théorique (CPT), Aix-Marseille University, and author of the bestselling Seven Brief Lessons on Physics

Big Bang theory has become a popular topic, but who knows the scientists who first proposed the outrageous concept that our entire universe started as an ultra-dense fireball? Theoretical physicist Jean-Pierre Luminet, well-known for his pioneering work on the visualization of black holes, takes the reader through a pedagogical, and historically accurate, tour of the conceptual vistas opened by the inventors of Big Bang theory, namely: the Russian mathematician (and meteorologist) Alexander Friedmann, the Belgian cosmologist (and priest) Georges Lemaître, and, last but not least, the eclectic genius physicist George Gamow. A must-read for any person eager to understand one of the major scientific breakthroughs of twentieth-century physics.

Thibault Damour, Institut des Hautes Études Scientifiques, recipient of the Einstein medal, the Galileo Galilei medal, and the Balzan prize

Astronomy, History of Science & Epistemology, My books & articles, Sciences

Cosmogenesis (9) : The Big Bang Discovery

1 Comment

Sequel of the preceding post Cosmogenesis (8) : The Nebular Hypothesis

Star Clusters and Nebulae. This page from "Telescopic views of Nebulae and Clusters by the Earl of Rosse and Sir J. Herschel" (1875) includes a variety of drawings of nebulosities by different observers. There are star clusters and gaseous nebulae (now known to belong to our own galaxy) as well as other galaxies. Observational techniques of the time were unable to distinguish between these very different types of objects.
Star Clusters and Nebulae. This page from “Telescopic views of Nebulae and Clusters by the Earl of Rosse and Sir J. Herschel” (1875) includes a variety of drawings of nebulosities by different observers. There are star clusters and gaseous nebulae (now known to belong to our own galaxy) as well as other galaxies. Observational techniques of the time were unable to distinguish between these very different types of objects.

In the first quarter of the 20th century cosmology became a distinct scientific discipline, thanks in part to the theoretical advance made in 1915 by Einstein with his theory of general relativity and in part to the revolution in observational techniques which revealed the true extent of the universe. Having at last been able to measure the distance of certain spiral nebulae, Edwin Hubble could confirm in 1925 that there existed other galaxies like our own.

His colleague Vesto Slipher had previously discovered that the radiation from these galaxies was constantly shifting towards the red end of the optical spectrum, which suggested that they were moving away from us at great speed. This movement was not understood until scientists came to accept an idea based on the theory of general relativity and first proposed by Alexandre Friedmann in 1922 and independently Georges Lemaître in 1927: that space was constantly expanding and consequently increasing the distance between galaxies. This idea proved to be one of the most significant discoveries of the century[i].

Alexander Friedmann in 1922
Alexander Friedmann in 1922

In an article which appeared in 1922, entitled “On the Curvature of Space“, Friedmann took the step which Einstein had balked at: he abandoned the theory of a static universe, proposing a “dynamic” alternative in which space varied with time. For the first time the problem of the beginning and the end of the universe was couched in purely scientific terms. Friedmann suggested that the universe was several tens of billions of years old, much older than the earth (then estimated to be about one billion years old) or the oldest known celestial objects. It was a remarkable prediction, the most recent estimate for the age of the universe being between 10 and 20 billion years.

In 1927, in a seminal article entitled “A Homogeneous Universe of Constant Mass and Increasing Radius Accounting for the Radial Velocity of Extra-Galactic Nebulae“, Lemaître explained the observations of Hubble and Slipher by interpreting them, within the context of general relativity, as manifestations of the expansion of the universe. This expansion was taking place uniformly across the entire universe (which might be finite or infinite), not outwards from a particular point (in this sense the often quoted analogy of a balloon being inflated is misleading). It was not a case of matter moving within a fixed geometric framework, but of the framework itself dilating, of the very “fabric” of space-time stretching. Continue reading →

History of Science & Epistemology, Sciences

The Rise of Big Bang Models (4) : Lemaître

1 Comment
Sequel of previous post : Dynamical solutions

In this series of posts about the history of relativistic cosmology, I  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaître, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaître, although his papers remain mostly  unquoted.

The discovery of expanding space

The 1920’s were precisely the time when the experimental data began to put in question the validity of static cosmological models. For instance, in 1924 the British theorist Arthur Eddington pointed out that, among the 41 spectral shifts of galaxies as measured by Vesto Slipher, 36 were redshifted ; he thus favored the de Sitter cosmological solution while, in 1925, his PhD student, the young Belgian priest Georges Lemaître, proved a linear relation distance-redshift in de Sitter’s solution. The same year 1925, Edwin Hubble proved the extragalactic nature of spiral nebulae. In other words, he confirmed that there existed other galaxies like our own, and the observable Universe was larger than previously expected. More important, the radiation from the faraway galaxies was systematically redshifted, which, interpreted as a Doppler effect, suggested that they were moving away from us at great speed. How was it possible ?

Arthur Eddington (1882-1944)
Arthur Eddington (1882-1944)

Young-Lemaitre
The young Georges Lemaître

It was Lemaître who solved the puzzle. In his 1927 seminal paper Un univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extragalactiques, published in French in the Annales de la Société Scientifique de Bruxelles, Lemaître calculated the exact solutions of Einstein’s equations by assuming a positively curved space (with elliptic topology), time varying matter density and pressure, and a non-zero cosmological constant. He obtained a model with perpetual accelerated expansion, in which he adjusted the value of the cosmological constant such as the radius of the hyperspherical space R(t) constantly increased from the radius of the Einstein’s static hypersphere RE at t = – ∞. Therefore there was no past singularity and no « age problem ». The great novelty was that Lemaître provided the first interpretation of cosmological redshifts in terms of space expansion, instead of a real motion of galaxies : space was constantly expanding and consequently increased the apparent separations between galaxies. This idea proved to be one of the most significant discoveries of the century. Continue reading →

History of Science & Epistemology, Sciences

The Rise of Big Bang Models (3) : Friedmann’s Dynamical solutions

3 Comments
Sequel of previous post : Static Solutions

In this series of posts about the history of relativistic cosmology, I  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaître, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaître, although his papers remain mostly  unquoted.

The Friedmann’s pioneering work

expanding-friedmannIn an article which appeared in 1922, entitled On the Curvature of Space (see Luminet 2004 for reference and translation), the Russian physicist Alexander Friedmann took the step which Einstein had balked at : he abandoned the theory of a static universe, proposing a “dynamic” alternative in which space varied with time. As he stated in the introduction, “the goal of this notice is the proof of the possibility of a universe whose spatial curvature is constant with respect to the three spatial coordinates and depend on time, e.g. on the fourth coordinate.“

friedmann-equation
The Friedmann’s Equation. R is the curvature radius of space, rho the mass density, Lambda the cosmological constant, k the sign of the space curvature, G the gravitational constant, c the speed of light

Thus he assumed a positively curved space (hypersphere), a time variable matter density and a vanishing cosmological contant. He obtained his famous “closed universe model”, with a dynamics of expansion – contraction. Continue reading →

History of Science & Epistemology, Sciences

The Rise of Big Bang Models (2) : Static solutions

Leave a comment
Sequel of previous post :  From Myth to Science

In this series of posts about the history of relativistic cosmology, I  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaître, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaître, although his papers remain mostly  unquoted.

The History of Relativistic Cosmology can be divided into 6 periods :

– the initial one (1917-1927), during which the first relativistic universe models were derived in the absence of any cosmological clue.

– a period of development (1927-1945), during which the cosmological redshifts were discovered and interpreted in the framework of dynamical Friedmann-Lemaître solutions, whose geometrical and mathematical aspects were investigated in more details.

– a period of consolidation (1945-1965), during which primordial nucleosynthesis of light elements and fossil radiation were predicted.

– a period of acceptation (1965-1980), during which the big bang theory triumphed over the « rival » steady state theory.

– a period of enlargement (1980-1998), when high energy physics and quantum effects were introduced for describing the early universe.

– the present period of high precision experimental cosmology, where the fundamental cosmological parameters are now measured with a precision of a few %, and new problematics arise (nature of the dark energy, topology of the universe, new cosmologies in quantum gravity theories, etc.)

Let us follow chonologically the rather hectic evolution of the ideas in the field. Continue reading →

Plastic arts

Luminet’s Illuminations

Gallery 2 Comments

Luminet’s reinstated visualization of a finite Universe, albeit one from which we can exit through one face and simultaneously enter through the opposite one, relies upon a keplerian form of mental sculpture that may be described as plastic rather than algebraic. Luminet’s characteristic lithograph, Big Bang, exploits the spatial vocabulary of perspective to evoke realms beyond the three dimensional. Whereas Escher relied on contradictions and oscillating ambiguity in his graphic art, Luminet suggests plunging, interpenetrating and matter organizes itself into structures on the right; the tumbling dice on the left imply irreversible disorganization arising from chance. The remarkable range of Luminet’s creativity in art and science is integral to his agenda to recreate what he calls a « humanism of knowledge » — not that the arts and sciences are somehow to be conflated, because they work in very different ways, with illogical and logical means. But Luminet argues that they well up from the same instincts and intuitions: « I do not believe that we acquire at the beginning the ‘heart of an artist’ or the ‘heart of a scientist’. There is simply within oneself a single devouring curiosity about the world. This curiosity pushes us to explore it through various languages and modes of expression, » he says.

Martin Kemp, professor of the history of art at the University of Oxford. Excerpt from “Luminet’s Illuminations : Cosmological Modelling and the Art of Intuition”, Nature, 20 november 2003, vol. 426, p. 232

History of Science & Epistemology

The Rise of Big Bang Models (1) : from Myth to Science

1 Comment

In this series of posts about the history of relativistic cosmology, I’ll  provide an epistemological analysis of the developments of the field  from 1917 to 2006, based on the seminal articles by Einstein, de Sitter, Friedmann, Lemaitre, Hubble, Gamow and other main historical figures of the field. It appears that most of the ingredients of the present-day standard cosmological model, including the accelation of the expansion due to a repulsive dark energy, the interpretation of the cosmological constant as vacuum energy or the possible non-trivial topology of space, had been anticipated by Lemaitre, although his papers remain mostly  unquoted.

 From Myth to Science

What are the origins of the universe, of the stars, of the earth, of life, of man? These questions have given rise to many different myths and legends, and today they are more than ever the subject of intensive research by astrophysicists, biologists and anthropologists. What were once fanciful stories are now scientific models; but whatever form they take, ideas about the origins of the universe both reflect and enrich the imagination of the people who generate them. Every society has developed its own stories to explain the creation of the world; all of them are ancient myths rooted in religion.

Whereas in monotheistic religions God is believed to have existed before the Creation, in most other kinds of religion the gods themselves are thought to originate from a creative element such as Desire, the Tree of the Universe, the Mundane Egg, Water, Chaos or the Void.

Tiamat-Marduk
Marduk slays the chaos dragon, Tiamat, in the Babylonian creation epic (British Museum, London)

A belief in some such primordial element, of which there are traces in every culture, underlies man’s thinking about the history of the cosmos like a primitive universal symbol buried in the collective subconscious. This may explain the vague links that can always be discerned between this or that creation myth and modern scientific descriptions of the origin of the universe –for example, big bang theory. There is therefore nothing mysterious or surprising about these correspondences other than that certain ways of thinking about the world should be so ingrained in the human mind.

An interesting approach, by the scientist and philosopher Wolfgang Smith (published in 2012)
An interesting approach, by the scientist and philosopher Wolfgang Smith (published in 2012)

In fact scientific and mythical explanations of the origins are neither complementary not contradictory; they have different purposes and are subject to different constraints. Mythical stories are a way of preserving collective memories, which can be verified neither by the storyteller nor by the listener. Their function is not to explain what happened at the beginning of the world but to establish the basis of social or religious order, to impart a set of moral values. Myths can also be interpreted in many different ways. Science, on the other hand, aims to discover what really happened in historical terms by means of theories supported by observation. Often considered to be anti-myth, science has in fact created new stories about the origin of the universe: big bang model, the theory of evolution, and the ancestry of mankind. It is therefore hardly surprising that the new creation stories developed by scientists tend to be regarded by the general public as modern myths.

Continue reading →