Tag Archives: Riemann

History of Science & Epistemology, My books & articles, Sciences

Non-Euclidean Geometries

3 Comments

This post is an adaptation of a chapter of my book  “The Wraparound Universe” with many more  illustrations.

************************************************************************

Thus we may perhaps, one day, create new Figures
that will allow us to put our trust in the Word,
in order to traverse curved Space, non-Euclidean Space.
Francis Ponge[1]

The oldest known fragment of Euclid’s Elements as part of the Oxyrhynchus papyri, dated from the Ptolemaic period and belonging to the famous Alexandrian Library

 

In book I of the Elements,[2] Euclid poses the five “requests” that, according to him, define planar geometry. These postulates would become the keystone for all of geometry, a system of absolute truths whose validity seemed irrefutable. One of the reasons for this faith is that these postulates seem obvious: the first of them stipulates that a straight line passes between two points, the second that any line segment can be indefinitely prolonged in both directions, the third that, given a point and an interval, it is always possible to trace out a circle having the point for its center and the interval as its radius, the fourth that all right angles are equal to each other. The fifth postulate is however less obvious:

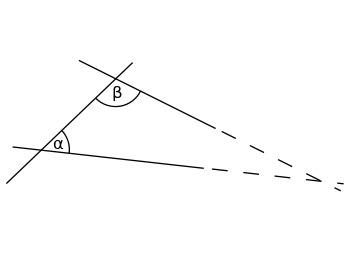
As the sum of the interior angles α and β is less than 180°, according to the fifth postulate the two straight lines extended indefinitely, meet on that side.

“If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.”

 

 

Although the statement does not refer explicitly to parallel lines, the the fifth postulate is currently called “Parallel postulate”. This can be better understood given the more popular version of the fifth postulate due to the Scottish mathematician John Playfair (1748-1819), who demonstrated that it was equivalent to the one given by Euclid : “Given a straight line and a point not belonging to this line, there exists a unique straight line passing through the point which is parallel to the first“.

A picturesque English edition of Euclid’s Elements by Oliver Byrne, 1847.

 

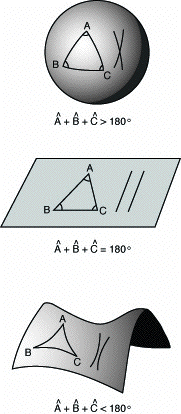Since the “parallel postulate” was more complicated than the others, the mathematicians following Euclid would try, for many centuries, to prove it from the four preceding ones, all in vain. In the nineteenth century, there occurred one of the great sudden revolutions in the history of mathematics (and also in human thought, as will be seen by what follows): two new geometries which do not satisfy the fifth postulate, but which are perfectly coherent, were discovered. In one of these geometries, called spherical geometry, no parallel line satisfying the conditions can be traced. This is the case for the surface of a sphere; the straight lines become great circles, whose planes pass through the center of the sphere, and since all great circles intersect each other at two diametrically opposed points (in the manner of the terrestrial meridians, which meet at the poles), no “straight line” can be parallel to another.[3] In the other geometry, called hyperbolic geometry, through any given point there passes an infinite number of lines parallel to another straight line. Continue reading →

Astronomy, History of Science & Epistemology, My books & articles

A brief history of space (3/4) : from Descartes to Schwarzschild

1 Comment
Sequel of the preceding post A Brief History of Space (2/4) : From Ptolemy to Galileo

At the beginning of XVIIth century, the way was open for new cosmologies, constructed on the basis of infinite space. Until then, the notion of space was conceived in the cosmological and physical order of nature, and not as the “background” of the figures and geometric constructions of Euclid. In other terms, physical space was not mathematicized. It became so thanks to René Descartes (1596 – 1650), who had the idea of specifying each point by three real numbers: its coordinates. The introduction of a universal system of coordinates which entirely criss-crossed space and allowed for the measurement of distances was a reflection of the fact that, for Descartes, the unification and uniformization of the universe in its physical content and its geometric laws was a given. Space is a substance in the same class as material bodies, an infinite ether agitated by vortices without number, at the centers of which were held the stars and their planetary systems.

A portrait of René Descartes

This new conception of the cosmos upset philosophical thought and led it far from the initial enthusiasm of the atomists and Giordano Bruno: “The absolute space which inspired the hexameters of Lucretius, the absolute space which that had been a liberation for Bruno, was a labyrinth and an abyss for Pascal.”[5] As for the scholars, they did not allow themselves to be discouraged by these moods and irresistibly moved towards the infinite universe.

The Descartes system of the world using vortices

The tendency toward the radical geometrization of an infinite space, initiated by Descartes, was consummated by the Englishman Isaac Newton (1642-1727). Newton postulated an absolute space, encompassing not only the background space of mathematics and the physical space of astronomy, but also that of metaphysics, since space was the “sensorium of God.” Physical space, finally identified with geometrical space, was necessarily Euclidean (the only one known at the epoch), without curvature, amorphous and infinite in every direction. At the heart of this immobile framework, Newton explained celestial mechanics in terms of the law of universal attraction, from now on considered responsible for gravitation and the large scale structure of the Universe. With Newton, cosmology took root for more than two centuries in the framework of an infinite Euclidean space and an eternal time.

Newton around 1700

All the problems are not resolved in Newtonian cosmology, far from it. On the question of the distribution of stars in space, for example, Newton believed that they must occupy a finite volume since, he argued, if they occupied an infinite space, they would be infinite in number, the force of gravitation would be infinite, and the universe would be unstable. Newton moreover supposed that the stars were uniformly spread within a finite mass|like a galaxy, for example. But a problem of instability remained: since each celestial body is attracted by every other one, at the least movement, at the least mechanical perturbation, all the bodies in the universe would fall towards a unique center, and the universe would collapse. Newton’s universe is therefore only viable if it does not admit motion on the large scale: its space is rigid and its time immobile. Continue reading →