This post is an adaptation of a chapter of my book  “The Wraparound Universe” with many more  illustrations.

************************************************************************

Thus we may perhaps, one day, create new Figures
that will allow us to put our trust in the Word,
in order to traverse curved Space, non-Euclidean Space.
Francis Ponge[1]

 

In book I of the Elements,[2] Euclid poses the five “requests” that, according to him, define planar geometry. These postulates would become the keystone for all of geometry, a system of absolute truths whose validity seemed irrefutable. One of the reasons for this faith is that these postulates seem obvious: the first of them stipulates that a straight line passes between two points, the second that any line segment can be indefinitely prolonged in both directions, the third that, given a point and an interval, it is always possible to trace out a circle having the point for its center and the interval as its radius, the fourth that all right angles are equal to each other. The fifth postulate is however less obvious:

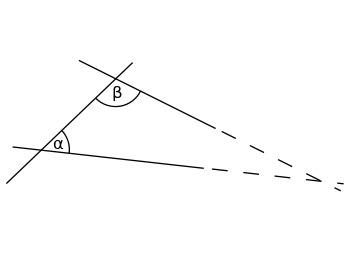
“If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.”

 

 

Although the statement does not refer explicitly to parallel lines, the the fifth postulate is currently called “Parallel postulate”. This can be better understood given the more popular version of the fifth postulate due to the Scottish mathematician John Playfair (1748-1819), who demonstrated that it was equivalent to the one given by Euclid : “Given a straight line and a point not belonging to this line, there exists a unique straight line passing through the point which is parallel to the first“.

 

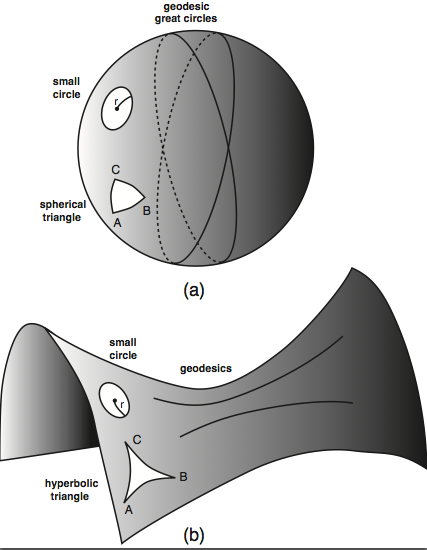
Since the “parallel postulate” was more complicated than the others, the mathematicians following Euclid would try, for many centuries, to prove it from the four preceding ones, all in vain. In the nineteenth century, there occurred one of the great sudden revolutions in the history of mathematics (and also in human thought, as will be seen by what follows): two new geometries which do not satisfy the fifth postulate, but which are perfectly coherent, were discovered. In one of these geometries, called spherical geometry, no parallel line satisfying the conditions can be traced. This is the case for the surface of a sphere; the straight lines become great circles, whose planes pass through the center of the sphere, and since all great circles intersect each other at two diametrically opposed points (in the manner of the terrestrial meridians, which meet at the poles), no “straight line” can be parallel to another.[3] In the other geometry, called hyperbolic geometry, through any given point there passes an infinite number of lines parallel to another straight line.

Euclid thus displayed uncommon depth of view. Not only is the fifth postulate indispensable, since it cannot be derived from the others, it is moreover this postulate that uniquely characterizes planar geometry. If it is infringed upon, the geometry is fundamentally changed in nature: now non-Euclidean, it allows one to model a space endowed with curvature.

Of course, three-dimensional Euclidean geometry already allowed one to speak of curvature with respect to objects of lesser dimension. It is obvious that the curvature of a circle, a one-dimensional space, becomes greater as the radius shrinks. Likewise for the sphere, a two-dimensional surface: the larger its radius, the weaker its curvature; in the limit, as its radius tends toward infinity, its curvature tends toward zero, which is to say that the sphere approaches the Euclidean plane. At any rate, in nature, planar geometry is an idealization. Most surfaces have a curvature which varies from one point to the other, being sometimes positive, sometimes negative: a hilly terrain, the surface of a piece of clothing, the surface of the human body, etc. But the discovery of non-Euclidean geometries allowed, for the first time in history, one to define in a coherent way a curved three-dimensional space, and as a consequence to use it to model the physical space in which we live.

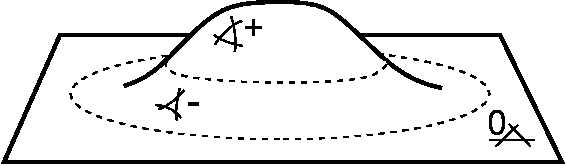
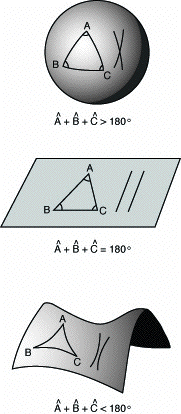
The parallel postulate allows two other equivalent formulations. One concerns the sum of angles in a triangle, the other the ratio between the circumference and radius of a circle. If the postulate is satisfied, it is strictly equivalent to dictating that the sum of the angles in a triangle is equal to 180 degrees and that the ratio of the circumference of a circle to its radius is equal to 2π –this is Euclidean geometry, with zero curvature. If no parallel can be traced, the sum of the angles in a triangle is greater than 180 degrees and the ratio of the circumference to the radius is smaller than 2π : one is in a spherical geometry, with positive curvature. If an infinity of parallels can be traced, the sum of the angles in a triangle is smaller than 180 degrees, the ratio of the circumference to the radius is greater than 2π, and one is in a hyperbolic geometry, with negative curvature.

The discoverers of non-Euclidean geometries were four mathematics geniuses named Lobachevsky, Bolyai, Gauss, and Riemann.

Nikolai Lobachevsky (1792–1856) was teaching at Kazan University, in Russia, when he published his results on an “imaginary geometry” (which would later be called hyperbolic), in 1829. One often reads that non-Euclidean geometries were conceived by way of pure mathematical speculation, without any reference to the physical universe. This is completely inaccurate. Lobachevsky, for example, declared that there was no branch of mathematics, no matter how abstract, that could not one day be applied to phenomena in the natural world. He used the best astronomical data of his time to calculate the sum of the angles in a cosmic triangle with three corners formed by stars. Of course, he found no difference from 180 degrees, but he remained convinced that there was nothing “natural” about Euclidean geometry. He would not live long enough to see the triumph of his ideas: after dismissal from his academic position in 1846, his health went into rapid decline.

Without being aware of Lobachevsky’s work, the Hungarian Janos Bolyai (1802–1860) developed hyperbolic geometry in a twenty-four page text entitled The Absolutely True Science of Space, as an appendix to a larger treatise written by his father, who was himself a mathematician. This accomplished violinist, fencer, and dancer in the imperial army of Austria, who fluently spoke nine languages, including Chinese and Tibetan, would leave behind twenty thousand pages of unpublished mathematical manuscripts. “ Out of nothing I have created a strange new universe,” he wrote, to which his father replied: “For God’s sake, please give it up. Fear it no less than sensual passions for it, too, may take all your time, and deprive you of your health, peace of mind, and happiness in life.”[4]

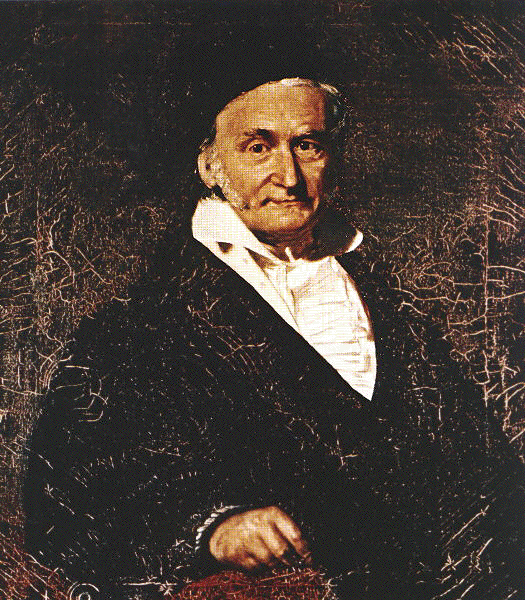
Carl Friedrich Gauss (1777–1855) taught himself to read and count at three years of age. Celebrated at first for his calculations and astronomical predictions, he became a professor at the University of Göttingen, where he established himself as the greatest mathematician of his time. He was also able to use his intelligence for practical ends: in the lecture hall of Göttingen, he carefully studied the financial news; thanks to judicious market speculations, he amassed a considerable personal fortune, which he administered with a masterly hand until his death. Gauss had made the same discoveries as Lobachevsky and Bolyai, several years before them; he wrote up some notes and sent some to friends in his letters, but did not dare to publish them officially. For him, in fact, non-Euclidean geometry could have no real existence.

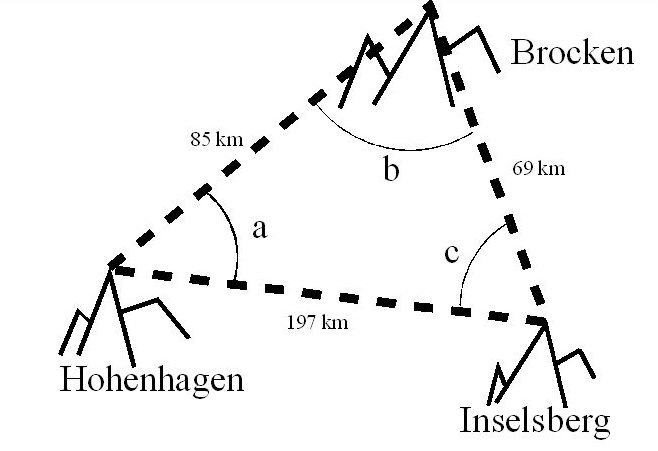
However, Gauss was the first to test the curvature of physical space by measuring the sum of the angles in a large triangle. Over the course of the 1820s, he made a precise survey of the triangle formed by the mountain peaks of Brocken, Hohenhagen, and Inselberg, in the south of Germany. The longest side measured about 100 km. Gauss found the sum of 179°59’59.32’’ and concluded that, up to observational errors, space in the neighborhood of Earth is Euclidean.

A modern version of Gauss’s method for directly measuring the curvature of space would be to launch six rockets in the plane of the equator, each one moving radially away from the Earth, while remaining perfectly equidistant to each other. One would thus have a series of equilateral triangles. If space is flat, the distance between each pair of rockets would grow while remaining equal to their distance from the Earth – which would also grow. If space is spherical, the distance between the rockets will grow more slowly than their distance to the Earth, while in the hyperbolic case their mutual distance would grow more quickly than their distance from us. This method combines the measurement of the sum of angles in a triangle and that of the circumference of a circle. In fact, the rockets would remain on a circle, with the effect that their mutual distances would reflect the augmentation of the circumference of the circle. Moreover, the angle formed by the straight lines which would connect each pair of adjacent rockets would be greater or less than 60 degrees (the value for flat space), according to whether the curvature of space was positive or negative.

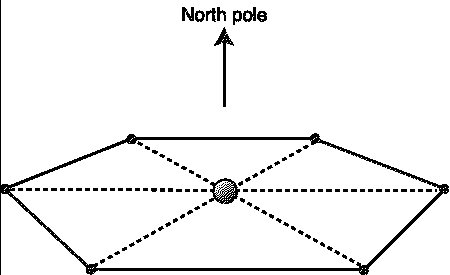
It would probably be useless to attempt this experiment; in fact, the difference from Euclidean geometry depends on the size of the triangle used with respect to the radius of curvature of space. The larger the triangle, the more important the difference|if there is a difference. It is obvious that a bacterium living on the surface of a large balloon does not perceive the curvature and has the impression of living on a plane. In the twentieth century, general relativity has taught us that, due to the smallness of the gravitational field caused by the Earth or by the Sun, the curvature of our surrounding space is so weak that a triangle of 100 km is much too small to show it. Any other method for locally measuring the curvature would run into the same difficulties, unless carried out near a black hole or at the surface of a neutron star, which for us is – at least for the moment– totally inaccessible.

Present-day observations teach us that the average radius of curvature of the Universe is at least 10 billion light years. Would we need to send rockets on a voyage at the speed of light for several billion years in order to form triangles that are sufficiently large to have a hope of directly revealing the curvature of the Universe? Luckily, no! Measurements of this type can be carried out, not with rockets, but with natural objects already placed at a good distance and equidistant to each other: the warm spots of the fossil radiation. This method has recently been used (the Boomerang, Maxima, and WMAP experiments) to set limits on the curvature of cosmic space.

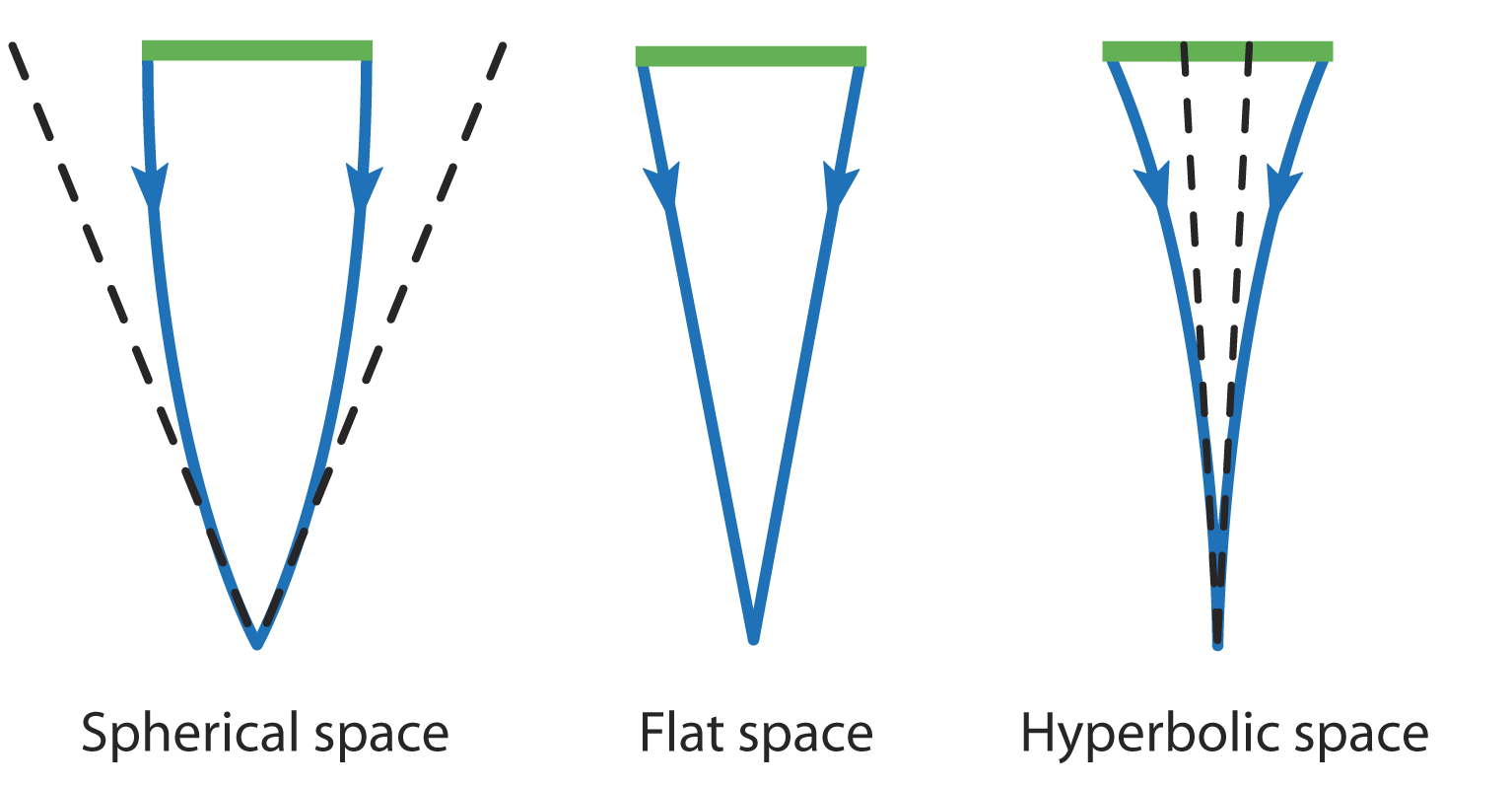
Strangely, Gauss, Lobachevsky, and Bolyai did not think to clarify the consequences of the inverse hypothesis, in which the sum of the angles in a triangle is greater than 180 degrees. It had been known, however, since antiquity that, on a sphere, the sum of the angles for a triangle made up of three arcs of great circles (the equivalent of straight lines) is always greater than 180 degrees. This spherical trigonometry had been the subject of innumerable treatments, at first useful for astronomy, and then for geography and navigation. The celestial vault in fact offers a spherical concavity, and if one wants to mentally trace a straight line between two stars, one must use an arc of a celestial great circle centered on the Earth. In the same way, if one desires to travel from one point of the terrestrial surface to another one which is very distant, the only authorized paths are situated on the convex surface: their is no question of digging a direct tunnel through the interior of the planet. The shortest possible path is thus an arc of a great circle, a fact well known to navigators.

One could have thus noticed that spherical trigonometry, in two dimensions, led to a coherent geometry, although it was not Euclidean. Why the resistance against passing to higher dimension? Probably because this implies a physical space which is finite but without frontier, encircled by straight lines. Now, up to this point, geometry had not been the science of space, but the science of figures in space. As a homogeneous, indefinite expanse of three dimensions, physical space constituted a neutral reality which gave rise to no speculation. This picture had been established in the eighteenth century by the philosophy of Kant, when he made Euclidean space a category of reason.

We must wait for Bernhard Riemann (1826{1866) for the acceptance of the validity of spherical geometry in three-dimensional space. In 1854, the young mathematician gave his inaugural dissertation at the University of Göttingen entitled: « On the Hypotheses which Lie at the Basis of Geometry ». The story of this lecture is an astonishing anecdote which shows how the sciences, just like universal history, sometimes progress unexpectedly through small accidents and fortuitous circumstances. At an age of twenty-seven years, Riemann wished to teach at Göttingen; to demonstrate his abilities, each candidate had to present an oral dissertation in front of the grand assembly of the university. The rules asked that each candidate propose, some time in advance, three subjects, among which the professors chose that which seemed most promising. Traditionally, it so happened that the professors always selected one of the two first subjects on the list. Riemann had therefore carefully prepared his two first subjects and slightly neglected the last, which in fact concerned the foundations of geometry. However, he had not accounted for the presence in the jury of the great Gauss who, although a septuagenarian, remained the dominant figure on the faculty. Naturally, Gauss felt that the third subject was the most interesting. Panicked at the prospect of this seminar, on which his entire career depended, Riemann threw himself madly into the preparation of his lecture and subsequently fell ill, to the point that he missed the date of presentation and only recovered his health in April. He then prepared his lecture for seven weeks, an amount of time that Gauss had requested as an adjournment for medical reasons. Riemann finally delivered his oral dissertation on June 10, 1854.

It was in this lecture that he demonstrated the possibility of a geometry in which space is finite without having a frontier: “The unboundedness of space possesses in this way a greater empirical certainty than any external experience. But its infinite extent by no means follows from this; on the other hand if we assume independence of bodies from position, and therefore ascribe to space constant curvature, it must necessarily be finite provided this curvature has ever so small a positive value. If we prolong all the geodesics starting in a given surface-element, we should obtain an unbounded surface of constant curvature, i.e., a surface which in a flat manifoldness of three dimensions would take the form of a sphere, and consequently be finite.”[5]

Riemann also proposed to extend geometry to spaces having an arbitrary number of dimensions. For this, geometry must be understood as the study of possible varieties. In the most general sense, a variety is nothing more than a collection of objects from a set. Geometry then becomes the study of the rules and conditions placed on the objects from the set in order to determine the distances between elements.

For example, in a two-dimensional space, each point is define in a unique way by an ordered pair of real numbers (x₁,x₂): its coordinates. In threedimensional space, each point is defined by a triplet of numbers (x₁,x₂,x₃). In an abstract n-dimensional space, each point has a unique address given by an n-tuplet (x₁,x₂,x₃,…. x_n), an ordered set of n real numbers. The rules for determining the distances between elements in the set are summed up by the metric, a sort of generalization of the Pythagorean theorem whose coefficients determine the curvature of the space.

Riemann is not only the creator of the most profound lecture in the history of geometry, but in 1858 he accomplished an exploit of the same order, with a completely innovative article of eight pages, on number theory. Perhaps he would have performed a third exploit, if he had not died of tuberculosis at thirty-nine years of age.

Riemann’s inaugural dissertation was not published until after his death, in 1867. Another year passed before the Italian Eugenio Beltrami (1835–1900) crowned the edifice of non-Euclidean geometry: his model of the “pseudosphere,” describing a hyperbolic space of constant negative curvature by means of an equation analogous to that of the hypersphere, put in evidence the common nature of the hypotheses of Bolyai and Lobachevsky, and of Riemann.

The way was now definitively opened for Clifford, Einstein, Weyl, and others to model certain natural phenomena like gravitation in terms of non-Euclidean geometry.

FURTHER READING

Rosenfeld, B. A., A History of Non-Euclidean Geometry, New York :Springer-Verlag, 1988.

FOOTNOTES

[1] Text on electricity, in “The Power of Language”, tr. S. Gavronsky, Berkeley: Univ. of California Press (1979)]

[2] see e.g. Euclid, Elements, T.L. Heath (transl.), Green Lion Press (2002).

[3] Let us remark that the sphere also does not satisfy either the first or second postulates: for two points situated at the antipodes, there are an infinity of straight lines passing from one to the other, and every straight line is of finite length (its circumference).

[4] Philip J. Davis and Reuben Hersch, The Mathematical Experience, Springer (2005)

[5] Transl. by W. K. Clifford, Nature vol.VIII, n° 183 & 184.