This post is an adaptation of a chapter of my book  “The Wraparound Universe” with many more  illustrations.

Expansion and the Infinite

Space alike to itself
that it grows or denies itself
Stéphane Mallarmé

The Universe is expanding. What does this really mean? Most people imagine an original huge explosion, as the term “big bang” suggests, and the metaphor is constantly used in popular accounts. Some speakers even have the tendency to mime a gesture of expansion with their hands, as if they were holding a piece of space or an immaterial balloon in the process of inflating. The public imagines some matter ejected at prodigious speeds from some center, and tell themselves that it would be better not to be there at the moment of explosion, so as not to be riddled through with particles.

None of all this is accurate. At the big bang, no point in the Universe participated in any explosion. Put simply, if one considers any point whatsoever, we notice that neighboring points are moving away from it. Is this to say that these points are animated by movement, given a speed? No, they are absolutely fixed, and nevertheless they grow apart.

To unravel this paradox, it is necessary to make more precise what one exactly means when speaking of a fixed point. The position of a point is fixed by coordinates: one number for a line (the miles along a highway), two numbers for a surface (latitude and longitude), and three for space in general (length, width, and height). A point is said to be fixed if its coordinates do not change over the course of time. In an arbitrary space, curved or not, the distance between two points is given by the so-called metric formula, which depends on the coordinates and generalizes the Pythagorean theorem. In principle, therefore, the distance between two points does not vary. In an expanding space, on the other hand, this distance grows, while the points do not move, even by a millimeter, meaning that they strictly conserve the same coordinates. These fixed coordinates are known as “comoving” coordinates. In relativistic cosmology, galaxies remain fixed at comoving positions in space. They may dance slight arabesques around these positions, under the influence of local gravitational fields, but the motion which moves them apart from each other resides in the literal expansion of the space which separates them.

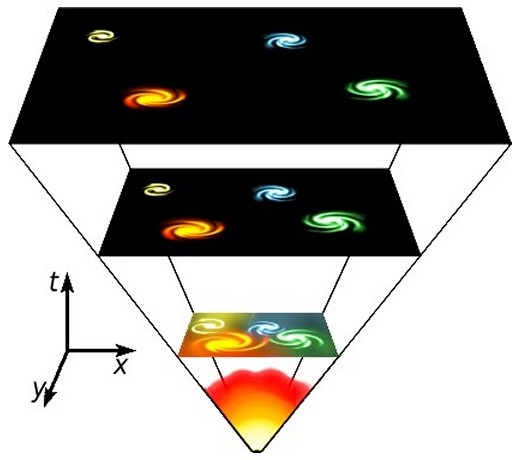It is a form of motion that no human being has experienced. It is therefore not surprising that our intuition rebels against its implications, and seeks other less radical interpretations. Thus, when Friedmann in 1922 and Lemaître in 1927 discovered that the expansion of the Universe was rendered possible by the laws of general relativity, and became convinced that this model should describe physical reality, they met many detractors – first and foremost among them being Einstein himself!

If space is expanding, it would seem at first sight that it must be finite: either because one visualizes some sort of big balloon which inflates into an external space, or because one starts from the principle that an expanding thing must necessarily grow in size and that, if this thing has a size, it is necessarily finite. One might also deduce, incorrectly, that at the big bang the Universe as a whole was necessarily contracted into a point of zero volume.

However, infinite systems may perfectly well expand or contract. How can something which occupies an infinite space dilate, and starting from what? This is one of the questions asked of me most frequently. In an attempt to explain, let us begin with a very simple example, that of a one-dimensional infinite universe: mathematically, it would be a straight line, on which each galaxy would be represented by a number.

At a certain instant (time A), the galaxies are separated by equal intervals, which means that their distribution is homogeneous. If the Universe is expanding, at the following instant (time B) the galaxy initially denoted by 1 occupies the position which galaxy 2 had, while galaxy 2 is now found where galaxy 4 initially was, and so on. We are really dealing with a uniform expansion within an infinite space containing an infinite number of galaxies. If one goes back in time to describe the big bang, all of the galaxies approach each other, and when they are all touching, space is still represented by a straight line of infinite length!

In generalizing to three dimensions, one can in the same way imagine that if space is infinite the big bang, meaning the beginning of expansion, began at every point of a space that was infinite beforehand, as compressed as it may have been. If one cuts infinite space into cubes, then each of these cubes will in the future become a larger cube, or in the past a smaller cube; but no cube is the center of the infinite space.

How could an infinite space dilate or contract and still occupy the same volume? The German mathematician David Hilbert gave a simple analogy. He imagined a hotel containing an infinite number of rooms, all of them occupied. A new customer arrives. Where do we put him? Fear not! The receptionist only has to transfer the occupant of room 1 into room 2, that of room 2 into room 3, and so on. The last to arrive can take possession of room number 1. Let us now imagine that car after car of tourists unload, an infinite number of them. Here again, the receptionist can perfectly well satisfy everybody: he moves the occupant of room number 1 to room number 2, that of number 2 into room number 4, that of room number 3 into number 6, and so on. In this way, one out of every two rooms will now be free (each room with an odd number)!

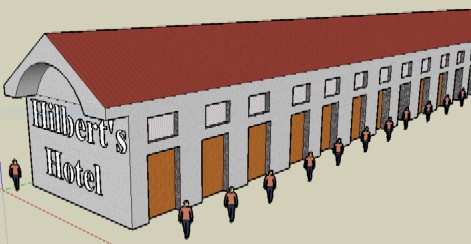
Just as in Hilbert’s hotel, an infinite space can accept an additional amount of space without becoming more “cramped.”