This post is an adaptation of a chapter of my book  “The Wraparound Universe” with many more  illustrations.

 

Galaxies in Flight

                     The spawning galaxy in flight is a rainbow trout which goes
back against the flow of time towards the lowest waters, towards the dark retreats of duration.
Charles Dobzynski (1963)

Since the time of Newton, we have known that white light, passing through a prism, is decomposed into a spectrum of all colors. Violet and blue correspond to the shortest wavelengths or, equivalently, to the largest frequencies; red corresponds to the largest wavelengths and to low frequencies. In 1814, the German optician Joseph von Fraunhofer discovered that the light spectrum from stars is streaked with thin dark lines, while that from candlelight has bright stripes. These phenomena remained puzzling until 1859. It was then that the chemist Robert Bunsen and the physicist Gustav Kirchhoff analyzed the light created from the combustion of different chemical compounds (burned with the now-famous Bunsen burner) and saw that each of them emitted light with its own characteristic spectrum.

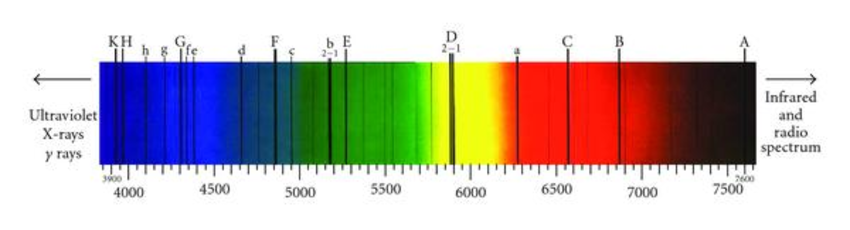
At nearly the same time, Christian Doppler discovered in 1842 that moving the source of a sound produced shifts in the frequency of sound waves, a phenomenon experienced by anyone listening to the siren of an ambulance passing by. The French physicist Armand Fizeau noticed the same phenomenon with light waves: depending on whether a source of light was moving closer or farther away, the received frequencies are either raised or lowered with respect to the emitted frequencies. The shift becomes larger as the speed of displacement is increased. If the source is getting closer, the frequency grows, and the light becomes more “blue”; if it moves away, the frequency lowers and the wavelengths stretch out, becoming more “red,” with respect to the spectrum of visible light. Since this shift affects the whole spectrum by the same amount, it is easily quantified by looking at the dark or bright stripes, which are shifted together, either towards the blue or towards the red, and it furnishes an incomparable means of measuring the speed of approach or retreat for light sources.

Shortly after this discovery, astronomers began an ambitious program of spectroscopy, with the aim of measuring the speed of the planets and stars by using their spectral shifts.

The formula for the Doppler-Fizeau effect is quite simple: v = cz, where v is the speed of the source, c the speed of light (300,000 km/s) and z the relative shift in wavelength λ, that is to say the difference between the received wavelength and the emitted wavelength, divided by the emitted wavelength.
[For those who like mathematical  formulae: z =(λ₀ – λ_e)/λ_e, where λ₀ is the observed wavelength and λ_e the emitted wavelength. We see immediately that if the source moves away, z is positive, while if it is getting closer, z is negative.]

The proper speeds of celestial bodies, whether planets, stars, or galaxies, is no more than a few hundred kilometers per second, which is small with respect to the speed of light. The Doppler-Fizeau effect is therefore weak, and requires precise spectroscopy to be measured. But let us imagine for a moment a universe where the speed of light would only be 1,000 km/s; the starry sky would offer an extraordinary spectacle to the eye: the stars would change color, those that flee would change into rubies, and those that approach into amethysts!

In the second decade of the twentieth century, American astronomers such as Vesto Slipher and Milton Humason  applied the program of systematic measurement of speed to the spiral galaxies – which produce spectral shifts similar to those of stars [1]. As long as the speeds deduced from the Doppler-Fizeau formula were no more than a few hundreds of kilometers per second, nobody questioned the fact that the spectral shifts of galaxies indicated the speed of their movement with respect to the Earth, just as for stars.

However, over the course of the 1920s spiral galaxies were discovered whose spectral shifts, systematically oriented towards the red, were greater than 0.1, which implies speeds of flight of more than 30,000 km/s! In a letter addressed to de Sitter in 1931, Hubble announced his preoccupation: “ We use the term “apparent velocities” in order to emphasize the empirical features of the correlation. The interpretation, we feel, should be left to you and the very few others who are competent to discuss the matter with authority.”

In fact, it was Georges Lemaître who, in 1927, was the first to understand that the redshift of galaxies did not correspond to physical speeds: it is space that is dilating, dragging galaxies along with it in an apparent motion of flight.

 

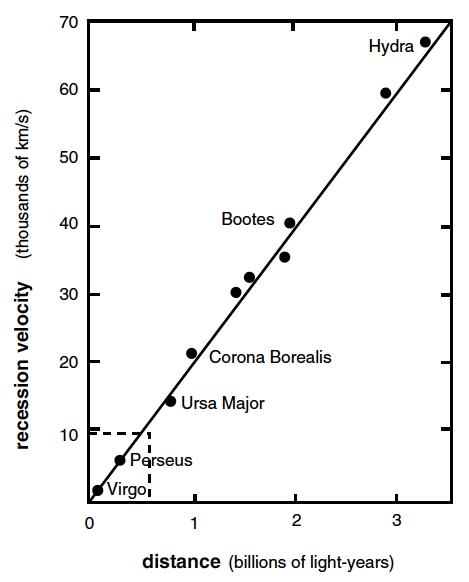
Although the theoretical perspective found itself radically changed, it remained nevertheless tempting to interpret these redshifts through the Doppler-Fizeau effect. The terms recession velocity or speed of flight were rapidly adopted by the astronomers and popularizers. These speeds seemed to be a completely natural consequence of the expanding motion of matter from the big bang. One pictured an initial firework throwing galaxies to the four corners of the Universe, like debris from an explosion. Perched on one of the cooled embers, we would be contemplating the other embers, moving away from us at great speed. However, this image is erroneous and leads to a completely false physical interpretation of the cosmological redshift. In fact, as astronomers explored the Universe more and more deeply, it turned out that the galaxies they detected were affected with redshifts that were ever larger. In 1930, Hubble was worried by redshifts of 0.1, but what can one say today of the quasar discovered in early 2,000 with z =5.82 ? As techniques progress, the records fall, month after month. The most recent data from the Hubble space telescope and the European VLT (Very Large Telescope) in Chile mention galaxies whose spectral shift is 10. This means that they are observed such as they were 13.2 billion years ago, when the Universe was only 500 million years old!

If one believes the formula for the Doppler-Fizeau effect, these galaxies must be receding at speeds five or six times greater than that of light, which is of course absurd. According to the theory of relativity, no object can travel faster than light. Even in a Newtonian model of the Universe, where speed would not be bounded by any limit, any observed galaxy would necessarily have a speed of flight smaller than that of light: if this were not so, its light rays would not have the time to reach us, since the distance to cover would grow faster than their speed!

The formula for the Doppler-Fizeau effect is therefore incapable of accounting for the cosmological redshift. A number of teachers of physics and astronomy believe themselves to be doing the right thing by appealing to the formula known as the “relativistic Doppler-Fizeau effect,” which corrects the regular formula in a way such that galaxies at large spectral shift now have speeds that are smaller than that of light.
[Again, for the lovers of formulae: 1 + z = (1+ v/c)/ √(1 – v²/c²)]

 Their idea is that at high speed special relativity is substituted for Newtonian mechanics, if one wants to correctly interpret the world. Indeed, by using the relativistic formula, a quasar at z = 4 only has a speed of flight equal to 92% of the speed of light, and everything seems to once again be in order. Nevertheless, they have done no more than to replace one incorrect explanation by another. To calculate the speed of the quasar in this way presupposes that special relativity is applicable on cosmological scales; however, this is a theory of flat space-time without gravity, while in cosmology the curvature of space-time plays a primary role (Even if space has zero curvature, the Universe as a space-time has a non-zero curvature as soon as it is in expansion).

Ascribing cosmological redshifts to a Doppler-Fizeau effect, either relativistic or not, leads to an unfortunate lack of understanding of big bang cosmology, and causes one to miss one of its most mysterious beauties.

Big bang cosmology is founded on the theory of general relativity, which transcends both Newtonian mechanics and special relativity, and introduces concepts which have no equivalents in these older theories. These concepts are not easily accessible to the general public, since our intuition is forged by natural processes that take place in a world moving at small velocity with weak gravity.

Just as the constancy of the speed of light leads to surprising but true statements, such as the twin paradox, the curvature of space-time leads to its own menagerie of phenomena. One of them involves the slowing-down of clocks in a gravitational field. This gravitational redshift is produced when the wavelength of light emitted from a massive body is shifted towards longer wavelengths during its journey toward the observer. This shift has nothing to do with any kind of Doppler-Fizeau effect, since the observer is not in relative motion with respect to the body emitting the signal.

The cosmological redshift is in fact another such phenomenon specific to general relativity, which has no counterpart in either Newtonian physics or special relativity. According to the interpretation initially given by Lemaître, it is not caused by galaxies moving through space like projectiles, it is the spatial fabric itself that expands. The cosmological redshift results from the fact that the radius of curvature of the Universe was smaller in the past, when the Universe was younger. This radius of curvature is measured by a scale factor a, which could be, for example, the radius of a sphere that includes the observable universe. Since space expands, a grows over the course of time; the light rays coming from the past have been stretched along the way, between the moment they were emitted by a distant galaxy and the moment we detect them. The correct formula for the cosmological redshift becomes 1+ z = R₀/R_e where R₀ is the scale factor of the Universe today and R_e the scale factor of the Universe at the time when the light was emitted from the galaxy. It has been given for the first time by Georges Lemaître in 1927.

Now, there is no longer any contradiction. By exploring the more and more distant past of the Universe, big bang cosmology predicts a scale factor R_e tending towards zero, which in turn implies redshifts tending towards infinity.

Although the maximum values observed today for galaxies are around z = 10, modern cosmology has discovered a much older light source, whose redshift reaches 1100: the cosmological background radiation. This implies that it was emitted during an epoch when the scale factor was 1,100 times smaller than it is today.[2]

The frontier of the observable universe – the cosmological horizon – necessarily corresponds to the limit where the redshift is infinite. This does not prohibit that, in certain models of the Universe, space can be immense and accommodate galaxies situated hundreds of billions of light years away from us. However, we cannot receive any radiation from them: in terms of a speed of expansion, these distant regions move away at a speed greater than that of light (In general relativity, space can expand more quickly than light, because space represents neither matter nor energy.)

Notes

[1] The discovery of recession of galaxies is attributed to Edwin Hubble, who published in 1929 his infamous paper showing the velocity-distance relation. For this he used a sample of 24 redshifts, 20 of which measured by Slipher (that he did not quote!) and 4 by his assistant Humason.

[2] To deduce a corresponding time scale in the history of the Universe, as one often does in scientific popularizations, we must pass to a particular model whose curvature parameters, meaning the density and the cosmological constant, are fixed. For plausible values of these parameters, the time of emission occurred between 300,000 and 1 million years after the big bang.