Sequel of the previous post Geometry and the Cosmos (1): Kepler, from polyedra to ellipses
The Pre-Socratic Universe
Since He [Zeus] himself hath fixed in heaven these signs,
The Stars dividing; and throughout the year
Stars he provides to indicate to men
The seasons’ course, that all things may duly grow.
Aratus, Phaenomena, I, 18.
Although Kepler was the first to determine the motion of the planets by mathematical laws, his search for a rational explanation to the universe was anticipated by numerous earlier thinkers. Even before the time of Socrates a number of philosophers had broken away from accepted mythology and postulated the idea of universal harmony. From the sixth century BC increasingly rational and mathematical ideologies based on the laws of physics began to compete with the traditional belief that the world was controlled by gods with supernatural powers. Most of these thinkers attempted to describe natural phenomena in mechanical terms, with reference to the elements of water, earth and fire. The Ionian philosophers in particular developed new ideas about the heavens, whose signs were used by many of their compatriots to navigate between the islands. Their fundamental notion was that the universe was governed by mechanical laws, by natural principles which could be studied, understood and predicted.
It was Thales of Miletus who propounded one of the first rational explanations of the world, according to which the earth was separate from the sky. Anaximander and Anaximenes, both also natives of Miletus on the coast of Asia Minor, put forward different ideas, which nevertheless derived from the same rationale: they proposed the existence of cosmological systems, explained natural phenomena in terms of a small number of “elements”, and invented new concepts – Anaximander’s “equilibrium” and Anaximenes’ “compression” – which can be regarded as the first recognition of the force of gravity.
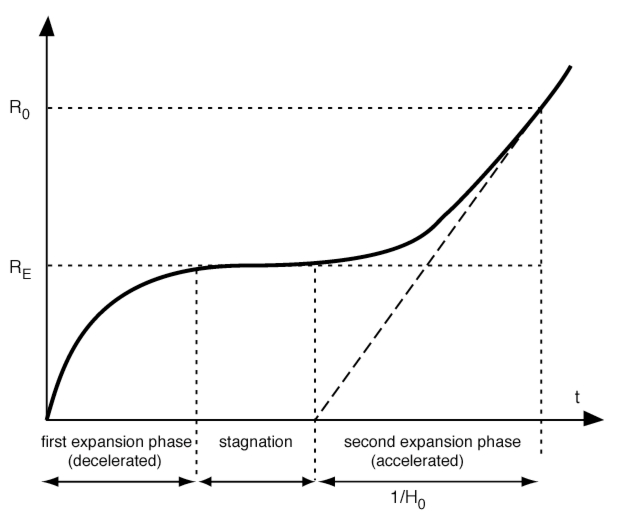
In Lemaître’s so-called “hesitating universe”, a cosmological model he devised in 1931 from Einstein’s field equations, the evolution of the cosmos is divided into three disctinct phases : two periods of rapid expansion are separated by a period of “stagnation”, representing a sort of equilibrium between the forces of gravitational contraction and expansion.
According to Heraclitus of Ephesus, the day was caused by exhalations from the sun, while the night was the result of dark emissions from the earth. The stars and the planets were bowls of fire which, when turned over, gave rise to eclipses and the phases of the moon. The moon itself, pale and cold, moved in the rarefied air above the earth, whereas the sun, our nearest star, was bright and hot.
Meanwhile, the Greeks were amassing measurements which would enable them to plot the stars more accurately. This required specialised instruments – gnomons to measure the sun’s shadow, compasses to fix the positions of the stars in the sky, etc. – as well as a system of notation which anyone could understand (previously the study of astronomy had been restricted to priests): how many fingers’ width above the horizon was such and such a star; where was due north, and so on. As well as mining the extensive archive of observations made by the Egyptians and Babylonians, the Greeks developed their own system of records. The pre-Socratic thinkers refined and analysed the basic ideas of their predecessors from Miletus with the result that the mechanistic view of the world gradually lost currency and a belief in underlying harmony became de rigueur. As early as 450 BC Anaxagoras of Clazomenae was accused of impiety for referring to the sun as a mass of hot metal, to the moon as a second earth and to the stars as burning stones – views no longer considered seemly.
Their theories on the workings of the universe led pre-Socratic thinkers to develop new ideas about the gods, astronomy, mathematics and universal harmony. But the last of these remained a mystery, which made it resistant to a scientific approach. “The cosmos, that most beautiful of all the things around us / An unseen harmony, more beautiful than the harmony we see / Nature loves to hide,” wrote Heraclitus in his De Natura Rerum.
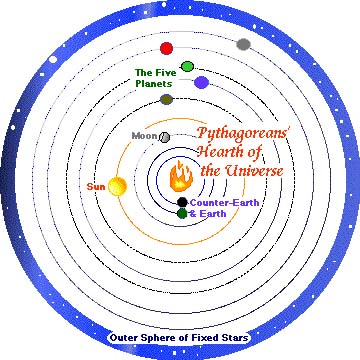
The Greek philosopher and mathematician Pythagoras was one of the first to eulogise on the subject of universal harmony, in the sixth century BC: “What is more rational? Numbers. What is more beautiful? Harmony.” This was the Pythagoreans’ petitio principii, on which they developed a cosmic theory based on numbers and harmony: the orbits of the planets and stars created resonances one with another, like notes in the scale.
Plato’s View
Supporting the great fortress of Harmony
The unique and perfect sphere of the earth
Stands proud, triumphant and solitary.
Empedocles’ Birth of the Elements.
The concept of universal harmony and a geometric view of the world are particularly relevant to the study of the sky. Such ideas gradually became more widely accepted even before Plato adopted the word kosmos – which had hitherto been used to describe women’s apparel (cf cosmetics), ornamentation, physical and moral attractiveness, order, poetry, truth, etc. – to denote the earth and stars. The cosmos was also the primary subject of poetry, the poetic world being a reflection of the real world, and became synonymous with the idea of a vast and majestic universe governed by the principles of aesthetics, order and harmony (the word “universe”, made up of the Latin unus and versus meaning literacy “facing one direction”, was used by Cicero to denote the whole of existence).
Plato’s concept of the cosmos enabled him to construct a compact and coherent model of the world. Following the Pythagoreans he created the first in a series of geometric models of the universe: a set of interlocking spheres representing a geocentric arrangement of stars and planets – a sphere being “the shape which incorporates all other shapes”, perfect, harmonious, symmetrical and uniform. These ideas are propounded in Plato’s Timaeus, his treatise on the aesthetics of cosmology.

Plato considered the physical world to be a single living entity consisting of the four elements of Empedocles, an imperfect reflection of the perfect world of ideas. Like Anaxagoras, Plato proclaimed the existence of a demiurge who was responsible for cosmic order. If man was to attain an understanding of this order, he must espouse the highest moral and intellectual ideals. “The true astronomer must be wiser than all the rest,” he wrote in his Epinomis. The time was past when the stars could simply be contemplated and their rising and setting merely observed: astronomy had to be approached in a scientific way, like mathematics and geometry, rather than from an aesthetic or artistic point of view. To study the stars for their beauty alone was to deprive oneself of their value as a tool. Advanced mathematics were required to plot the trajectories of the stars and Plato knew that the motion of the planets, as well as that of the sun and stars, was not random but obeyed certain laws and was therefore predictable; that was the starting point for the application of geometry to an understanding of the workings of the cosmos.


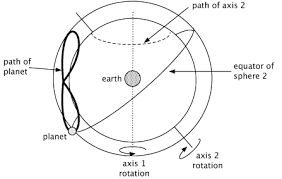
One of Plato’s pupils, the mathematician Eudoxus of Cnidus, whose skill at geometry was equal to his master’s demands, perfected the Platonic model of the cosmos by explaining the apparent motion of the planets in relation to combinations of uniform, circular movements – with the earth at their centre. Each of these circular movements was the result of the interaction between the motion of two spheres revolving at the same speed in opposite directions about independent axes. This aesthetically satisfying theory, known as the theory of homocentric spheres, appeared to explain all astronomical phenomena. Each planet required four spheres: one to account for its rotation about its own axis, one for its sidereal period, and two more for the anomalies in its motion (standstills, retrograde motion, etc.
The Two Worlds of Aristotle
Another of Plato’s pupils was even more determined to describe natural phenomena in rational terms. In his On the Heavens and Physics Aristotle propounds the notion of a geocentric universe which conforms to a hierarchic order, each of the celestial bodies belonging to a spherical layer and these layers fitting neatly inside each other, without any space between them, in the order Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, the stars.
It was Aristotle who introduced the fundamental distinction between sublunary and superlunary worlds. The former, including the earth itself, consists of the world of change and corruption: creatures and things are born, grow, wear out and die. The latter, comprising the heavens and the firmament, is the world of perfection, eternal and unchanging. This distinction would continue to be made until the early 16th century.

Parchment 13th century, Paris Mazarine Library.
In the case of the sublunary region, Aristotle adopted the ideas of Empedocles: that all matter is made from the four basic elements, earth, water, air and fire, and that everything has its natural place. The earth, being the heaviest element, belongs at the centre of the cosmos, which is therefore geocentric. Water, air and fire inhabit concentric layers surrounding the earth. All terrestrial matter tends towards the centre, inevitably creating a spherical shape. The earth is therefore a sphere (if the earth were not spherical, Aristotle argued, we would not see a curved boundary between light and shade on the moon during a lunar eclipse), although a relatively small one compared to the firmament, which is also spherical. Unlike the other celestial bodies, the earth is always stationary. If it were not, we would see the stars move by an effect of parallax (We now know that the stars are so far away that their parallactic motion seen from the earth is too small to habe been detected by Greek astronomers).
The superlunary region is made from a completely different substance. The celestial spheres are not convenient geometric shapes but consist of a transparent, crystalline substance: ether. This supernatural element – neither heavy nor light, neither created nor dissoluble, everlasting and unchanging – exists in its purest form in the superlunary region and deteriorates in the sublunary region. Unlike the four terrestrial elements, which move in straight lines, ether’s natural motion is circular. Beyond the sphere of the firmament, the Prime Mover, which is motionless, imparts motion to the spheres below. It is the origin of all movement, which is therefore natural, circular and uniform, neither accelerating nor decelerating (and all the more perfect for having neither beginning nor end).

Like Eudoxus and Callippus, Aristotle believed that each planet was accompanied by a number of spheres, although he considered his predecessors’ explanations to be inadequate. In order to maintain the balance of the planetary system, he proposed additional spheres which would interact with the existing ones. Although the addition of “retrograde” spheres (i.e. spheres turning in the opposite direction to the others) preserved the unity of the celestial model, it complicated rather than simplified the problem of planetary motion.
The next post will deal with Ptolemy’s theory of planetary motion

I think the picture shown of the Pythagorean model is actually that of his students. Pythagoras himself did not consider a rotation of the earth or a counter- earth
It is true that we have no direct information about Pythagoras original thinking, since he did not write any treatise. Thus the only description of “his” cosmology comes from his students. And in any case the picture shown is a much late (and pedagogical) reconstruction… Thanks Cormac for the reading and the comment.