Introduction
The regularity of so much celestial activity has led many cultures to base their models of the universe on concepts of order and harmony. Around the Mediterranean it was the Pythagoreans who first expressed the idea that the universe is characterised by proportion, rhythm and numerical patterns. Plato’s hypothesis was of an organised cosmos whose laws could be deciphered, explained in geometric terms.
The history of physics is nothing other than the story of man’s desire to uncover the hidden order and harmony of things. The most ambitious physicists have attempted to unify apparently discrete phenomena: Galileo with terrestrial and celestial laws; Newton with gravity and the movement of celestial bodies; Maxwell with magnetism and electricity; Einstein with space and time; today’s physists with gravitation and microphysics.
But, as Heraclitus said as long ago as 500 BC, “Nature loves to hide.” Indeed advances in geometry and mathematics have led to new theories of the cosmos which we are unable to comprehend. They provide only abstract images, which do not allow us to visualise the structure of atoms or the dynamics of space-time or the topology of the universe in any direct sense.
It is this fundamental belief in celestial harmony – for which successive generations have found various elaborate expressions: just proportion, equation of the part and the whole, symmetry, constancy, resonance, group theory, strings -that has underlain the development of physics for the past 2,500 years.

Geometry and the Cosmos
“Geometry, which before the origin of things was coeternal with the divine mind and is God himself […], supplied God with patterns for the creation of the world.”
Johannes Kepler, The Harmony of the World, 1619.
The 17th century German astronomer Johannes Kepler was undoubtedly the first to integrate man’s fascination with harmony into an overall vision of the world which can properly be called scientific. For Kepler, as for the natural philosophers of ancient Greece, the cosmos was an organised system comprising the earth and the visible stars. His avowed intention was to investigate the reasons for the number and sizes of the planets and why they moved as they did. He believed that those reasons, and consequently the secret of universal order, could be found in geometry. Kepler wanted to do more than create a simple model or describe the results of his experiments and observations; he wanted to explain the causes of what he saw. This makes him one of the greatest innovators in the history of science and it led him in particular to formulate laws of planetary motion which are still valid today.
Despite his innovative methods, Kepler wrote two studies of the cosmos in the style of the ancient Greeks: Mysterium Cosmographicum (The Secret of the Cosmos) in 1596 and Harmonices Mundi (The Harmony of the World) in 1619. At this turning point between ancient and modern thinking Kepler was steeped in a tradition which connected cosmology explicitly with the notion of divine harmony. But what Kepler sought to express was not the numerical mysticism of the Pythagoreans; his starting point was geometric patterns, which he saw as “logical elements”. His profound desire to devise a rational explanation for the cosmos led him to establish procedures which resembled those of modern science.
From Polyhedra to Ellipses
In the 1590s, when he was practising as a mathematician in Graz (then part of Styria) Kepler adopted the ideas of Copernicus. In the heliocentric model, which the Polish thinker had propounded fifty years earlier, the simultaneous motion of the earth around the sun and about its own axis explained the observed motion of the planets and stars. Kepler set out to prove that this simple hypothesis, which had been an attempt to “save the appearances”, did indeed correspond with reality. In doing so, however, he noticed that the circular orbits of the planets around the sun proposed by Copernicus were not in keeping with his precise observations. Being a fervent Christian, Kepler wanted at the same time to glorify God, who he believed was responsible for the harmonious arrangement of the universe (the cosmos, like the Bible, proclaiming the glory of God like a book without words whose secrets it was man’s duty to discover). This aim is stated in the very first lines of the preface to The Secret of the Cosmos: “It is my intention, reader, to show in this little book that the most great and good Creator, in the creation of this moving universe and the arrangement of the heavens, looked to these five regular solids, which have been so celebrated from the time of Pythagoras and Plato down to our own, and that he fitted to the nature of those solids the number of the heavens, their proportions and the law of their motions.” (1)
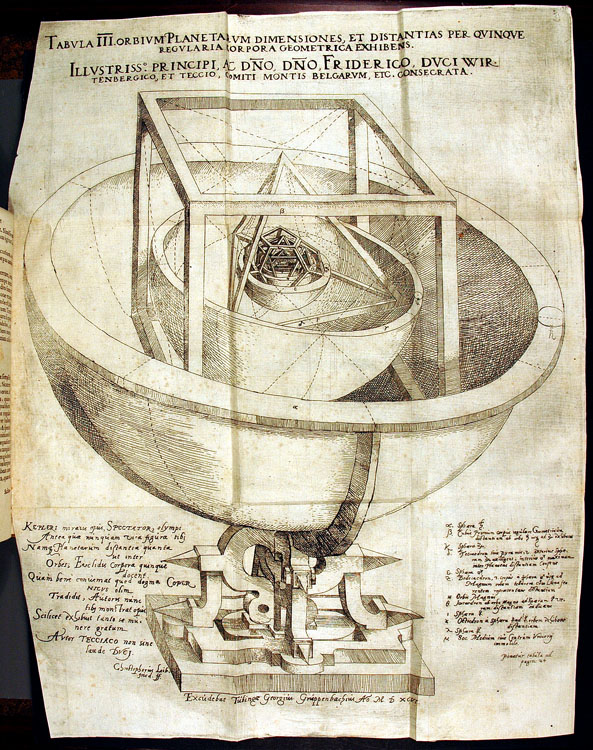
Kepler saw this divine harmony most clearly in the distribution of the planets and in their relative distances from the sun. Everything was an expression of that harmony: poetry and music as well as mathematics and geometry, which he claimed to be of fundamental importance. In this he can be seen as part of the great movement to reinstate mathematics as a tool for studying nature, a movement which was then in its infancy but which would later recruit even more radical followers like Descartes and Galileo. It was the latter who was to declare in The Assayer of 1623: “Philosophy is written in this grand book – I mean the universe – which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and to interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles and other geometrical figures, without which it is humanly impossible to understand a single word of it. Without these, one is wandering about in a dark labyrinth.” (2) This resurgence of mathematics would soon make numerology and numerical mysticism obsolete, just as the development of astronomy and astrophysics were to bring about the decline of astrology as a system of interpreting the universe.

In his Secret of the Cosmos Kepler applies geometry in a new way to solve the problem of the relationship between the planetary orbits. Using regular polyhedra, symmetrical geometric shapes familiar to the ancient Greeks, he argues that the five “perfect” solids (cube, octahedron, dodecahedron, tetrahedron and icosahedron), which Plato had used to represent the five elements (earth, water, air, fire and ether), should correspond exactly to the intervals between the six then known planets (Mercury, Venus, Earth, Mars, Jupiter and Saturn). He goes on to demonstrate mathematically how these Platonic shapes can be arranged one inside the other exactly in accordance with the structure of the solar system. For Kepler this was no coincidence: convinced that he had discovered “the secret of the cosmos”, he interpreted the correspondence between the planets and the polyhedrons as a novel and rational way of understanding the fundamental harmony of the universe.
In The Secret of the Cosmos Kepler justified his use of polyhedra at the same time as questioning the pre-eminence of the curve: “if at the Creation God had taken cognizance only of the curved, except for the Sun in the centre, which was the image of the Father, the Sphere of the Fixed Stars, or the Mosaic waters, at the circumference, which was the image of the Son, and the heavenly air which fills all parts of the space and the firmament, which was the image of the Holy Spirit – then, except for these, I say, nothing would exist in this cosmic structure.” (3) But, since so many other heavenly bodies exist, “we must of necessity seek the causes of them all in straightness” and specifically in regular polyhedra, whose perfection is synonymous with that of the celestial sphere.
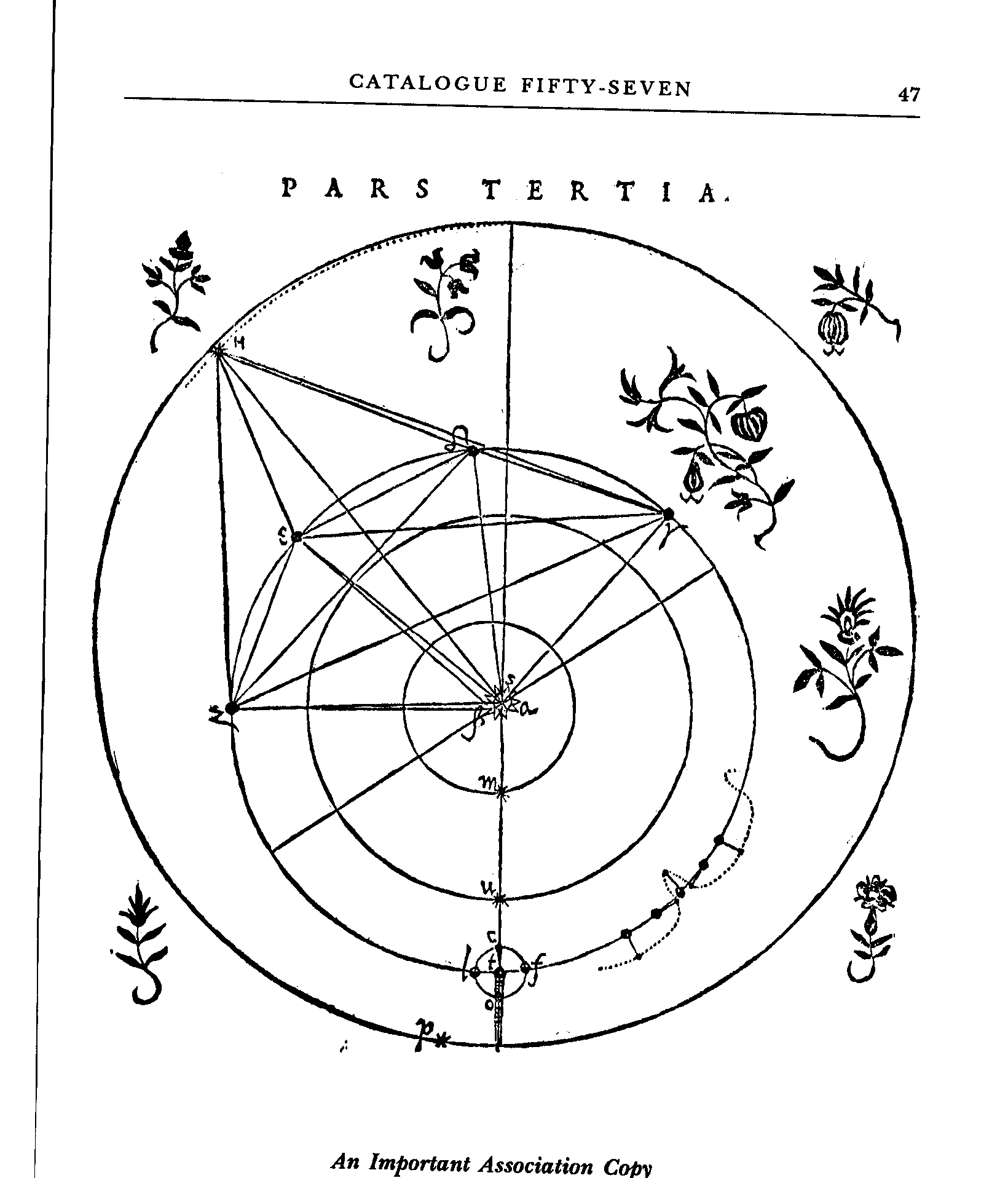
Johannes Kepler, Astronomia Nova, 1609.
Paris, BNF, Rare Books Archive, gV. 454, p. 149
Kepler would never be able to discard completely this quasi-mystical view of the cosmos, even though he abandoned the idea of a strict correspondence between the shapes of polyhedra and the orbits of the planets in 1609 when he discovered that those orbits were elliptical rather than circular and therefore would not fit into such a model. It was nevertheless his obsessive search for underlying harmony that led him to the laws of planetary motion, which more or less contradicted his initial ideas and which revolutionised the study of astronomy. In his Astronomia Nova (The New Astronomy) of 1609 Kepler modified the Copernican model of the solar system, shattering the belief in the perfection of circular orbits; he even went as far as suggesting that it is the sun’s influence which causes the planets to follow their orbits.
In The Harmony of the World Kepler finalised his laws of planetary motion. The third of these, known as the law of orbital periods, establishes a “harmonic” relationship, in the mathematical sense of the word, between the axis of the orbit and the orbital period and enables the movement of the planets to be described and calculated much more easily, without however explaining the physical causes of those movements. That task would fall to Isaac Newton, for whom cosmic harmony was a manifestation of universal laws of attraction.
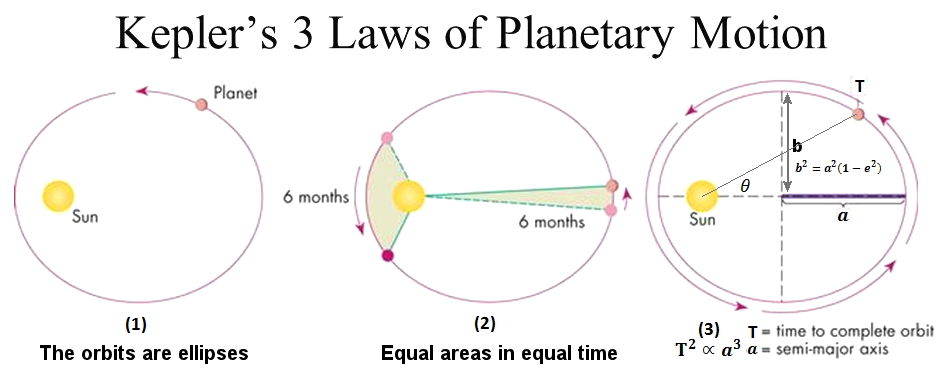
Kepler’s name is associated principally with the laws of planetary motion. The first two laws were published in his -New Astronomy, the third in The Harmony of the World. Their discovery excited him almost to the point of ecstasy: “A very few days after the pure Sun of that most wonderful study began to shine, nothing restrains me; it is my pleasure to yield to inspired frenzy.”
1.The Law of Elliptical Orbits
The orbit of each planet is an ellipse with the sun at one focus.
An ellipse with zero eccentricity is a circle; the greater the eccentricity, the more elongated the ellipse. In a highly eccentric orbit a planet will pass very close to the sun and then travel very far away from it.
2. The Law of Equal Areas
The planets move in such a way that their radius vectors sweep out equal areas in equal time.
The further a planet is from the sun, the more slowly it travels. The speed of a planet is directly related to its distance from the sun in that the area of the segment of the ellipse swept out in any given time is constant.
3. The Law of Orbital Periods
For each planet the cube of half the major axis of its orbit is equal to the square of its orbital period. This ratio applies regardless of the mass of the planet.
Kepler’s laws apply not only to the planets revolving around the sun, but to any body orbiting any other under the force of gravity (e.g. moons orbiting planets, artificial satellites orbiting the earth).
Kepler and Tycho Brahe
Kepler’s career was greatly affected by his meeting with the Danish astronomer, Tycho Brahe. In 1576 Brahe’s patron Frederick II, king of Denmark, had granted him permission to construct a magnificent house and observatory, a temple to astronomy called Uraniborg, on the island of Hven. Brahe designed the building according to the theory of “divine proportion”, which had been developed by the philosophers of the Italian Renaissance and applied to architecture principally by Palladio.

In his Great Atlas the Dutch cartographer Joan Blaeu published a series of maps of Europe based on the work of his father Willem Blaeu who, as a pupil of Tycho Brahe, had stayed at the Uraniborg observatory. In acknowledgement of Brahe’s influence, the Great Atlas contains enlargements of the series of colour plates which the Danish astronomer had included in his Astronomiae Instauratae Mechanica of 1598.
Uraniborg (meaning “castle of the heavens”) housed an entire community dedicated to the study of the sky whose organisation reflected the extraordinary personality of its creator. As well as the observatory itself there were workshops where astronomical instruments were made, a library, a laboratory, a paper mill and printing press, kitchen gardens, fish tanks, orchards, an irrigation system, a flour mill, etc. Uraniborg was where Tycho Brahe devoted himself to the observation of the sky. There he refined man’s knowledge of the moon, studied the refraction of light, constructed a revised star catalogue and recorded with unprecedented accuracy the positions of the planets.
Joan Blaeu, Atlas Major, Amsterdam, 1662.
After the death of his patron, Tycho Brahe fell into disgrace and left Uraniborg. He reestablished himself underthe patronage of the Holy Roman Emperor, Rudolf II, in Bohemia, where he invited Kepler to work with him. When Brahe died in 1601, it was Kepler who inherited the record of his uniquely detailed observations, working intensively on the information relating to the orbit of Mars. By 1605 Kepler had determined its shape: not a circle or a combination of circles, but an ellipse with the sun at one focus.

Tycho Brahe, whom Kepler described as “the prince of astronomers”, left behind magnificent engravings showing the astronomical instruments he had created in the workshops at Uraniborg and used at Stjerneborg, the observatory he built near it four years later. The most impressive of these was the giant mural quadrant (with a radius of 1.8 m) whose finely spaced graduations allowed the most precise measurements: to within a fraction of a minute of arc. The data he collected soon superseded those of Ptolemy and later enabled Kepler to discover the laws of planetary motion. The figure on the right represents Tycho Brahe himself taking a sighting through the skylight at the top left of the picture while his assistants record the time of the observation (below right) and enter the reading in a log (below left).
Tycho Brahe, Astronomiae Instauratae Mechanica,
Wandesburg, 1598.
References
(1) Johannes Kepler, The Secret of the Cosmos, trans. A. M. Duncan, Abaris Books, New York, 1981, p. 63.
(2) Galileo Galilei, The Assayer, translated by Stillman Drake and C. D. O’Malley, Univ. of Pennsylvania Press, 1960, pp. 183-84.
(3).Johannes Kepler, The Secret of the Cosmos, op. cit. p. 95.

“Geometry, […], supplied God with patterns for the creation of the world.” Johannes Kepler, The Harmony of the World, 1619.
Kepler would have agreed with Einstein that “The mathematical precision of the universe reveals the mathematical mind of God.” This is contrary to the commonly held, modern-day view that science and theism are incompatible. Yet, the strong evidence of fine-tuning, and the corresponding failure of naturalness theories, seems to support theism over materialism.
For sure Kepler was one of the greatest minds in the history of science. But at his time it was almost impossible to be outside the religious thinking. I don’t agree at all about the fact that in modern relativistic cosmology there are failures that would support theism; for instance the fine-tuning problem is a problem only because it is an ill-posed one! In any case, thanks for the reading and the comment, all reasonable opinions are welcome!
Naturalness problems are more than ill-posed, they are impossible to define. Underlying naturalness are assumptions about probability distributions which are neither knowable nor testable, because we only have one observable universe. Naturalness is itself based on the materialistic assumption that the properties of the observable universe, and indeed its very existence, are the result of random-chance processes. To me, this view is no more rational or realistic than the theistic view that the universe was specifically designed (fine-tuned) for life.
In the first version of Myst. Cosm. Kepler knows that the orbit of Mars is 687 days (more exactly 686 59/60 days). This is well before he has access to Tycho’s data, so how does he know this?
Copernicus did not know this.
So where did K get that number from?
It may be derived from the time between oppositions, 780 days, if he knew that then. Or, from Mars’ 42 circuits of the Zodiac in 79 years.
Yes. That’s how long it takes for Mars to move through the zodiac. This had to have been know for quite along time before these guys came along, as it can be observed relatively easily.