Introduction

Black holes are to many the most mysterious objects in space. According to the laws of General Relativity, they are by themselves invisible. Contrarily to non-collapsed celestial bodies, their surface is neither solid nor gaseous ; it is an immaterial border called the event horizon, beyond which gravity is so strong that nothing can escape, not even light.

Seen in projection on a sky background, the event horizon would have the aspect of a perfectly circular black disk if the black hole is static (the so-called Schwarzschild solution) or of a slightly distorted one if it is in rotation (the Kerr solution). Due to strong gravitational lensing, such a « bare » black hole could leave an observable imprint on a starry background. However, in typical astrophysical conditions, whatever its size and mass (ranging from stellar to galactic scales) a black hole is rarely bare but is dressed in gaseous material. Swirling in a spiral motion, the gas forms a hot accretion disk within which it emits a characteristic spectrum of electromagnetic radiation. Giant black holes, such as those currently lurking at the centers of galaxies, can be also surrounded by a stellar cluster, whose orbital dynamics is strongly influenced. As a matter of fact, , if a black hole remains by itself invisible, it “switches on” in its characteristic way the materials it attracts, and distorts the background starry field by gravitational lensing.

Thus, as soon as the basics of  black holes astrophysics developed in the 1970’s,  the scientists logically wondered what could look like a black hole. Many of you certainly saw didactic or artistic representations of a black hole in popular science magazines, in the form of a black sphere floating in the middle of a circular whirlwind of brilliant gas. So striking they are, these images fail to report the astrophysical reality. This one can be correctly described by means of numerical simulations, taking into account the complex distortions that the strong gravitational field prints in spacetime and light rays trajectories.

Since the first numerical simulations performed 40 years ago, tantalizing progress has been done to detect black holes through electromagnetic radiation from infalling matter or gravitational waves. The first telescopic image by the Event Horizon Telescope of the nearest giant black hole SgrA*, lurking at he center of our Milky Way galaxy, is expected for 2018.

The aim of this series of posts is to retrace the rich history of black hole imaging.

Preliminary steps

Black hole imaging started in 1972 at a Summer school in Les Houches (France). James Bardeen, building on earlier analytical work of Brandon Carter, initiated research on gravitational lensing by spinning black holes. Bardeen gave a thorough analysis of null geodesics (light-ray propagation) around a Kerr black hole. The Kerr solution had been discovered in 1962 by the New Zealand physicist Roy Kerr and since then focused the attention of many searchers in General Relativity, because it represents the most general state of equilibitum of an astrophysical black hole.

The Kerr spacetime’s metric depends on two parameters : the black hole mass M and its normalized angular momentum a. An important difference with usual stars, which are in differential rotation, is that Kerr black holes are rotating with perfect rigidity : all the points on their event horizon move with the same angular velocity. There is however a critical angular momentum, given by  a = M (in units where G=c=1) above which the event horizon would « break up » : this limit corresponds to the horizon having a spin velocity equal to the speed of light. For such a black hole, called « extreme », the gravitational field at the event horizon would cancel, because the inward pull of gravity would be compensated by huge repulsive centrifugal forces.

James Bardeen computed how the black hole’s rotation would affect the shape of the shadow that the event horizon casts on light from a background star field. For a black hole spinning close to the maximum angular momentum, the result is a D-shaped shadow.

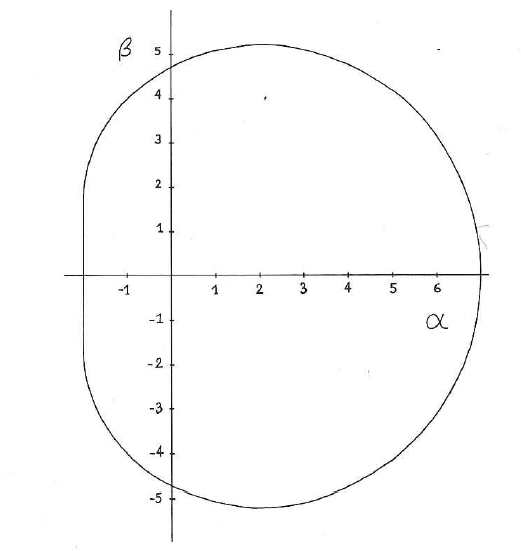
The reference is Bardeen, J. M. 1973, Timelike and null geodesics in the Kerr metric, in Black Holes (Les Astres Occlus), ed. C. Dewitt & B. S. Dewitt, (New York: Gordon and Breach) p.215–239

At the time, C.T. Cunningham was preparing a PhD thesis at the University of Washington in Seattle, under the supervision of Bardeen. He began to calculate the optical appearance of a star in circular orbit in the equatorial plane of an extreme Kerr black hole, taking account of the Doppler effect due to relativistic motion of the star, and pointed out the corresponding amplification of the star’s luminosity. He gave formulas but did not produced any image.
The reference is Cunningham, C.T. and Bardeen J.M., The optical appearance of a star orbiting an extreme Kerr black hole, ApJ 173 L137-142 (1972).

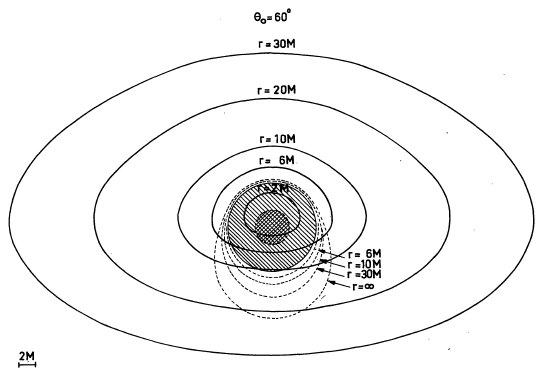
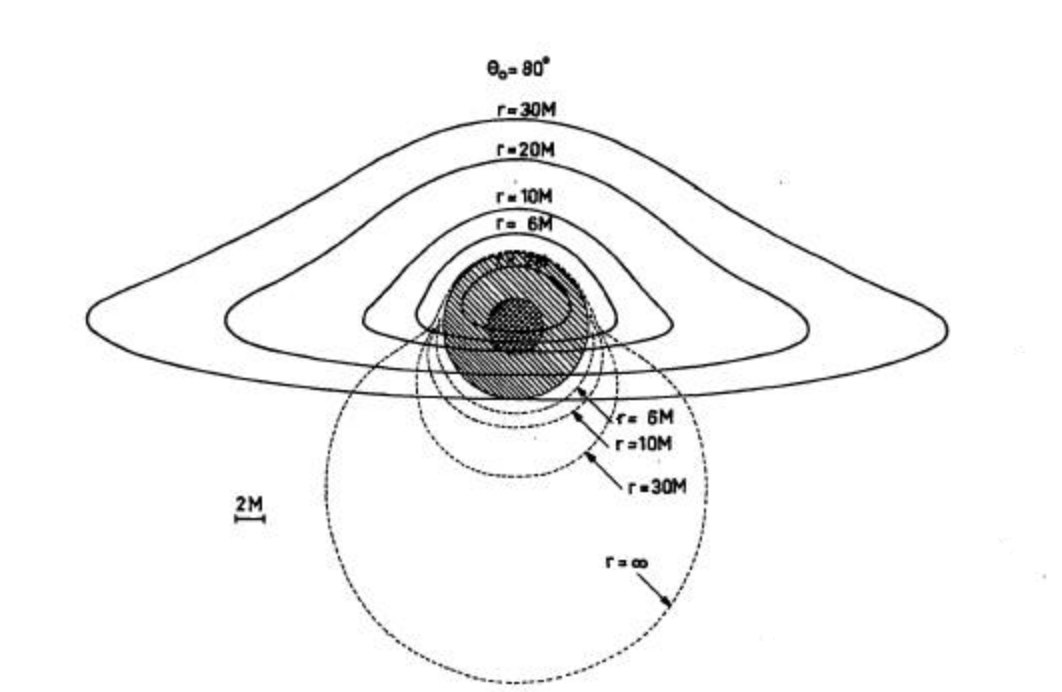
One year later Cunningham and Bardeen published a more complete article with the same title. For the first time a picture was shown of the primary and secundary images of a point source moving in a circular orbit in the equatorial plane of an extreme Kerr  black hole. They calculated as functions of time the apparent position and the energy flux of the point source as seen by distant observers.

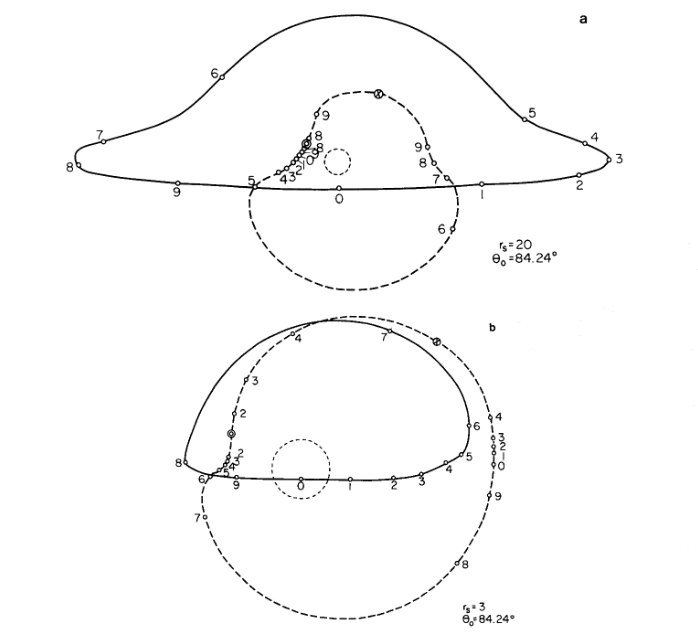
In the upper diagram showing the distorted image of a circle of radius  20M, we clearly see that, whatever the observer’s inclination angle, the black hole cannot mask any part of the circle behind. We also see that the black hole’s spin hardly affects the symmetry of the primary image (although the asymmetry is stronger for the secundary image).
The exact reference is Cunningham, C.T. and Bardeen J.M., The optical appearance of a star orbiting an extreme Kerr black hole, 1973, ApJ, 183, 237. The article can be uploaded here.

In 1975, Cunningham calculated the effects of redshifts and focusing on the spectrum of an accretion disk around a Kerr black hole. He gave formulas and drawed graphics but no image.
The reference is  Cunningham, C. T., The effects of redshifts and focusing on the spectrum of an accretion disk around a Kerr black hole, ApJ, 202, 788 (1975)

In 1978 Leigh Palmer, Maurice Pryce and William Unruh carried out,  for pedagogical purpose, a simulation of starlight lensed by a camera orbiting a Schwarzschild black hole, using an Edwards and Sutherland Vector graphics display at Simon Fraser University. They showed a film clip in a number of lectures in that period, but unfortunately they did not publish their simulation, so that I can’t reproduce here any image.

First calculations for a black hole accretion disk

The same year and quite independently, as a young researcher at Paris-Meudon Observatory specialized in the mathematics of General Relativity, I wondered what could be the aspect of a Schwarzschild black hole surrounded by a luminous accretion disk. Accretion disks are expected to form in some double-star systems that emit X-ray radiation (with black holes of a few solar masses) and in the centers of many galaxies (with black holes whose mass adds up to between one million and several billion solar masses). Their close-up images must experience extraordinary optical deformations, due to the deflection of light rays produced by the strong curvature of the spacetime in the vicinity of the black hole. General relativity and a computer allow the detailed calculation of such effects.

Thus I undertook to calculate the bolometric appearance (i.e. including the contributions at all electromagnetic wavelengths) of a thin accretion disk gravitationally lensed by a non-spinning black hole, as seen from far away, but close enough to resolve the image. I considered a Schwarzschild black hole and a physical model of a thin disk of gas viewed from the side, either by a distant observer or a photographic plate.

Throughout my researchers’s career I always considered that, before writing a computer program with complicated equations and running the machine, pure geometrical reasoning is of a great help to get a preliminary idea of the result. Otherwise, what guarantee have you that your program had no mistake ? I did this kind of geometrical reasoning to guess what I should obtain for the black hole’s accretion disk appearance. In an ordinary situation, meaning in Euclidean space, the curvature is weak. This is the case for the solar system when one observes the planet Saturn surrounded by its magnificent rings, with a viewpoint situated slightly above the plane. Of course, some part of the rings is hidden behind the planet, but one can mentally reconstruct their elliptic outlines quite easily. Around a black hole, everything behaves differently because of the optical deformations due to the space-time curvature, as depicted in the diagram below (published only years later in my popular book on black holes.

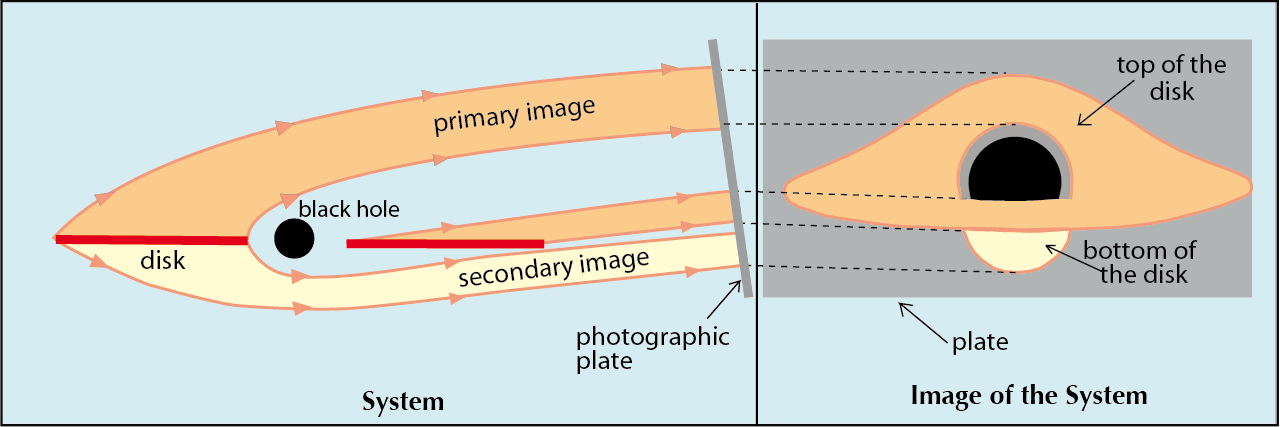
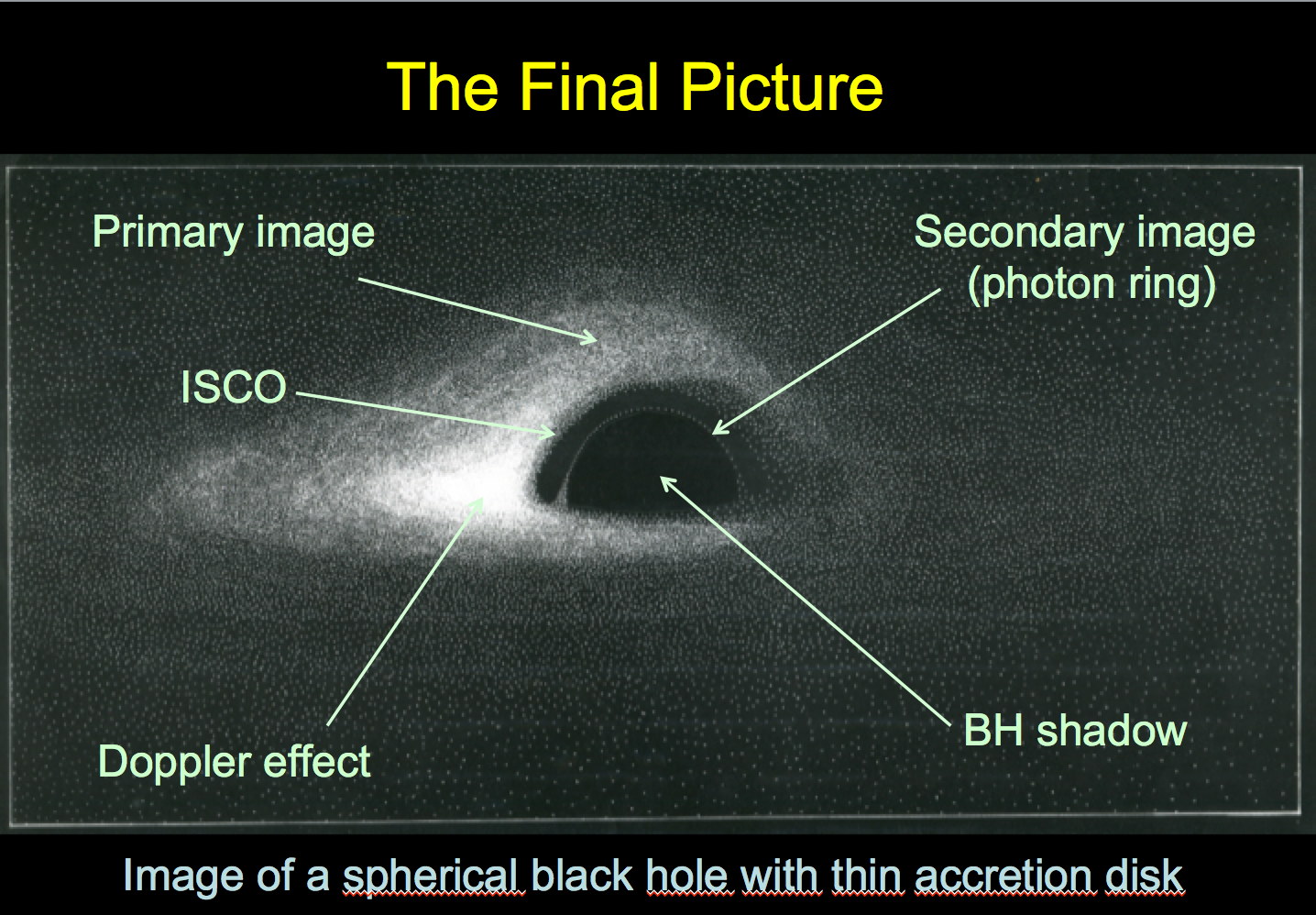
Strikingly, we can see the top of the disk in its totality, whatever the angle from which we view it may be. The back part of the disk is not hidden by the black hole, since the images that come from it are to some extent enhanced by the curvature and reach the distant observer. More astonishing, one also sees a part of the bottom of the gaseous disk. In fact, the light rays which normally propagate downwards, in a direction opposite to that of the observer, climb back to the top and give a « secondary image », a highly deformed picture of the bottom of the disk.

We also see that no radiation can come from the region between the black hole’s event horizon and the inner edge of the disk. Indeed the properties of the Schwarzschild space-time forbid the accretion disk from touching the surface of the black hole. The circular orbits of the gas in the disk can be maintained only down to a critical distance of three times the Schwarzschild radius (i.e. 6M). Below this the disk is unstable, the gas particles plunge directly towards the black hole without having enough time to emit electromagnetic radiation.

We also notice that the apparent size of the event horizon, called the “black hole shadow”, is larger than the real size by a factor 3√3 / 2 due to gravitational lensing, as is illustrated in the figure below (only the black and white figure was displayed in the original article, the coloured one was published much later in my book of 2006 “Le destin de l’univers”. 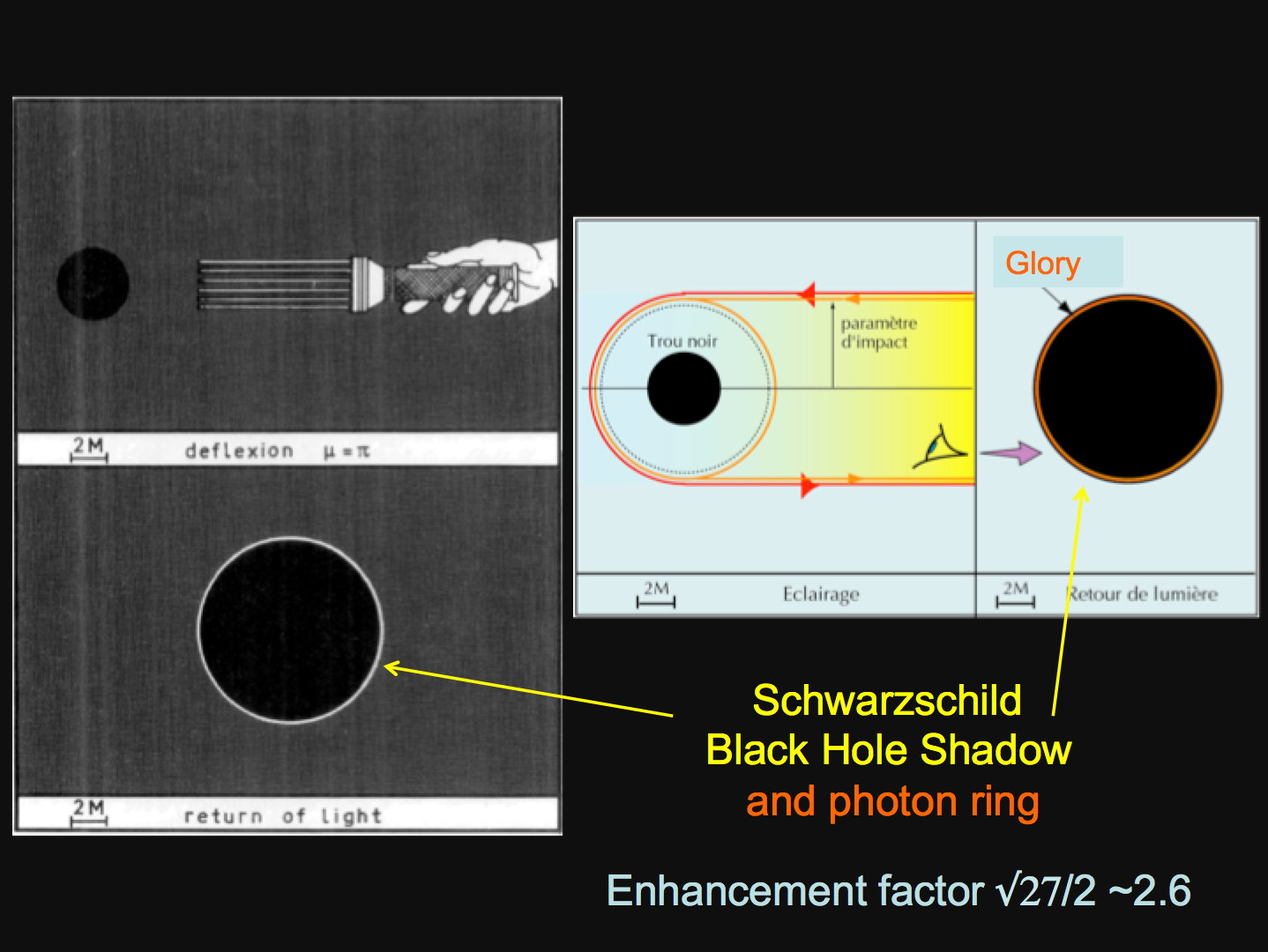 I called the photon ring the “black hole glory“, referring to the glory effect well known in traditional optics: when sunlight is scattered by innumerable water droplets in mist, it is sometimes possible to see in reflection the shadow of one’s own head surrounded by brilliant rings of light centred on the line of sight.

Then I could start to calculate the things. I used the IBM 7040 mainframe of Paris-Meudon Observatory, an early transistor computer with punch card inputs. The machine generated isolines that were directly translatable as smooth curves using the drawing software available at the time. The first step was to integrate the equations of light ray trajectories in Schwarzschild space-time and draw the isoradial curves (i.e. at constant radial distance from the black hole), as they would be seen by an observer above the disk’s plane.

In fact the gravitational lensing generates an infinity of images of the disk, because the light rays can travel any number of times around the black hole before escaping from its gravitational field and being observed by a distant astronomer. The primary image shows the upper side, the secondary image shows the lower side, the third image shows the upper side again, and so on. However, higher order images are not optically interesting because they are stuck to the edge of the central black spot, the latter representing the silhouette of the actual black hole expanded by a factor √3/2 ~ 2.6 .

By comparison with the image calculated by Cunningham and Bardeen for a circular ring at distance 20M around an extreme Kerr black hole (see above), we check that the spin of the black hole hardly affects the shape of the primary image.

The first virtual photograph

My next step was to take into account the physical properties of the gaseous disk : rotation, temperature and emissivity. When the flow of matter into a black hole is not too great, it forms a very thin accretion disk. In that case, the proper luminosity of the disk can be accurately calculated, according to models first described by Shakura and Sunyaev (1973) and by Page and Thorne (1974) in its relativistic version : the intensity of radiation emitted at any given point of the disk only depends on its temperature, and the latter only depends on the radial distance to the black hole. Therefore the intrinsic brightness of the disk cannot be uniform. The maximum luminosity comes from the inner regions close to the horizon, because it is there that the gas is the hottest.

In addition, the apparent luminosity of the disk will still be very different from its intrinsic one: the radiation picked up at a great distance is frequency- and intensity-shifted with respect to the emitted one. There are two sorts of shift effects. There is the Einstein effect, in which the gravitational field lowers the frequency and decreases the intensity. And there is the better-known Doppler effect, where the displacement of the source with respect to the observer causes amplification as the source approaches and attenuation as the source retreats. In this case, the disk rotating around the black hole causes the Doppler effect. The regions of the disk closest to the black hole rotate at a velocity approaching that of light, so that the Doppler shift is considerable and drastically modifies the image as seen by a faraway observer.

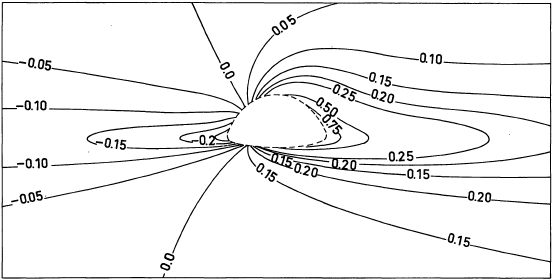
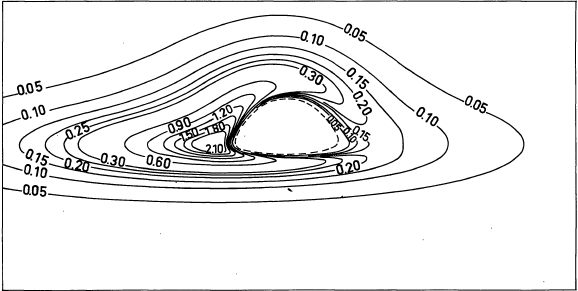
The combination of the two effects (Einstein and Doppler) is not trivial.  I calculated it at each point of my virtual photographic plate. The figure below depicts the curves of constant spectral shift, as seen by an observer at 10° above the plane of the disk

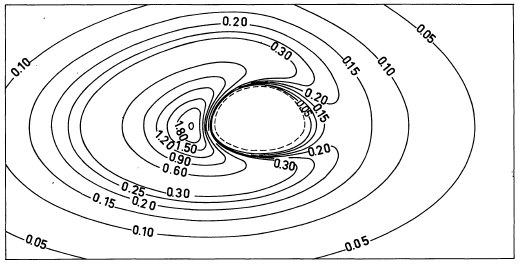
In order to obtain the final realistic photograph, I had therefore to correct the intrisic luminosity of the disk by the spectral shift effects. Figures below, from my 1979 article, depict the isophotes –  i.e. the  curves of constant apparent luminosity – as seen by an observer at respectively 30° and 10° above the disk’s plane.

 

The final black and white “photographic” image was obtained from these patterns. However, lacking at the time of an appropriate drawing software, I had to create it by hand. Using numerical data from the computer, I drew directly on negative Canson paper with black India ink, placing dots more densely where the simulation showed more light – a rather painstaking process! Next, I took the negative of my negative to get the positive, the black points becoming white and the white background becoming black. The result, The result converged into a pleasantly organic, asymmetrical form, as visually engaging as it was scientifically revealing.

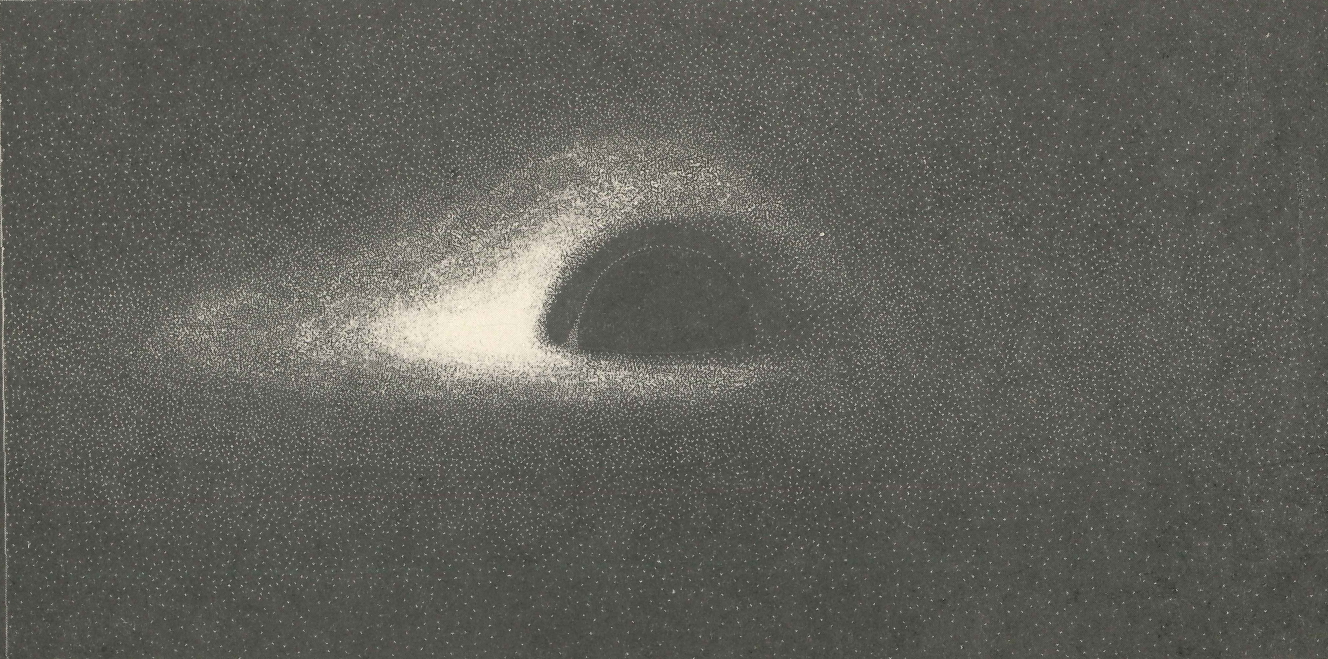
To better understand the various elements of the picture I’ve added below some text elements (not included in the orginal paper).

At the end of the paper I precised that the calculated images should be valid for a large number of black hole situations, namely black holes with any mass accreting matter at sufficiently low rate, such as for instance the supermassive black hole whose existence in the core of the galaxy M87 had recently been sugested.

My picture was first published in a popular article on black holes for a French magazine. The reference is B. Carter & J.-P. Luminet, Les Trous Noirs, Maelströms cosmiques, La Recherche n°94, 944, 1978)

The complete work was published a few months later, in English and with all the technical explanations, in the top-class European journal Astronomy & Astrophysics.

The reference is J.-P. Luminet : Image of a Spherical Black Hole with Thin Accretion Disk, Astron.Astrophys. 75, 228, 1979. The article can be uploaded here.

A rather funny anecdote is that, several years later, I was told that some readers who discovered my simulated picture of a black hole surrounded by a luminous disk believed that the mysterious author of the article used the name Luminet as a pseudonym !

Colours bloomed first in Japan

Despite this early work, gravitational lensing by black holes remained a backwater of physics research until a decade later.
In 1988 I travelled to Japan to attend an international conference in Tokyo.  Two young Japanese searchers came to me and, to my surprise, wanted to take o photograph of all three together. Indeed Jun Fukue and Takushi Yokoyama had just extended my work by adding (false) colours to the black hole picture, and  for them I was a kind of a pionneer!  This was a real improvement, since my monochromatic (because bolometric) image did not take into account the real change of apparent wavelengths in the accretion disk, shifted from blue on one side to red on the other, and so on.  Here are some of the pictures they produced  :

 

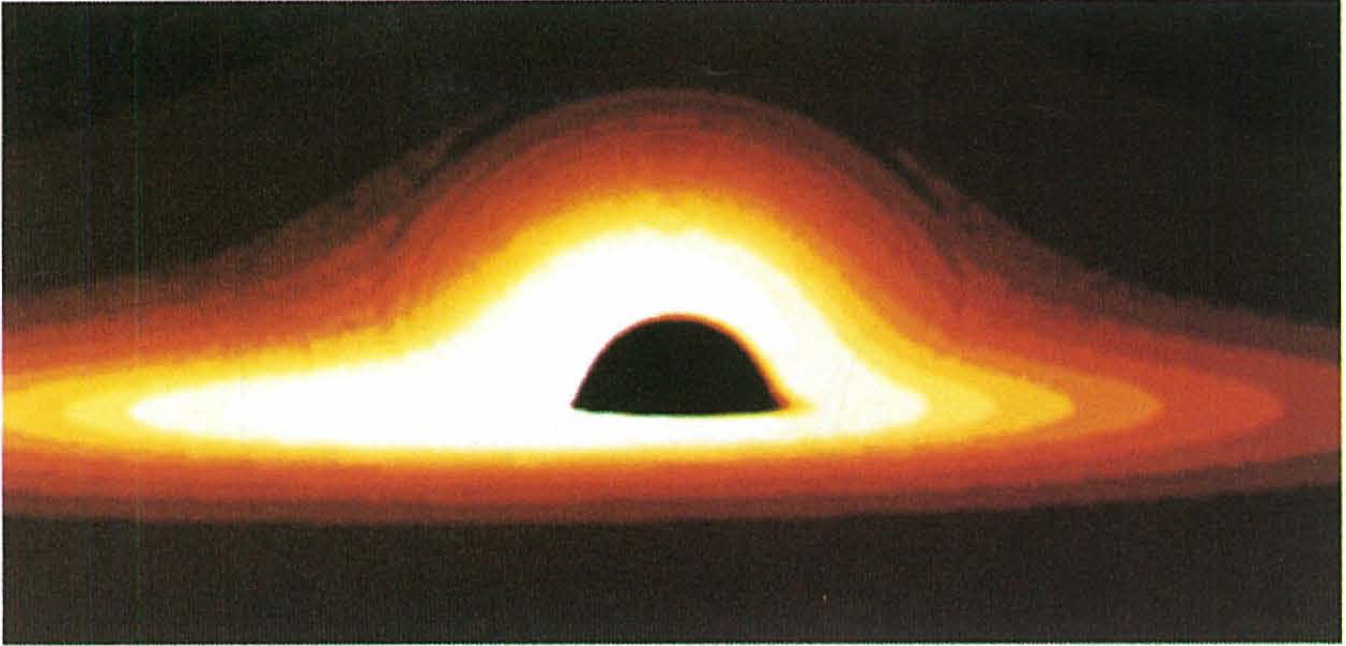
The reference is J. Fukue and T. Yokoyama : Colour photographs of an accretion disk around a black hole, Publ. Astron. Soc. Japan 40 15 (1988) (the article can be uploaded here).

Another funny anecdote is that in their manuscript, the authors initially used the term “Lady” for the “accretion disk”, but the editors replaced this by the “accretion disk” in accordance with the general style of the Publications of the Astronomical Society of Japan…

 

The second chapter of the story is here : (2) Colors and movies, 1989-1993