Sequel of the previous post Geometry and the Cosmos (1): Kepler, from polyedra to ellipses
The Pre-Socratic Universe
Since He [Zeus] himself hath fixed in heaven these signs,
The Stars dividing; and throughout the year
Stars he provides to indicate to men
The seasons’ course, that all things may duly grow.
Aratus, Phaenomena, I, 18.
Although Kepler was the first to determine the motion of the planets by mathematical laws, his search for a rational explanation to the universe was anticipated by numerous earlier thinkers. Even before the time of Socrates a number of philosophers had broken away from accepted mythology and postulated the idea of universal harmony. From the sixth century BC increasingly rational and mathematical ideologies based on the laws of physics began to compete with the traditional belief that the world was controlled by gods with supernatural powers. Most of these thinkers attempted to describe natural phenomena in mechanical terms, with reference to the elements of water, earth and fire. The Ionian philosophers in particular developed new ideas about the heavens, whose signs were used by many of their compatriots to navigate between the islands. Their fundamental notion was that the universe was governed by mechanical laws, by natural principles which could be studied, understood and predicted.
It was Thales of Miletus who propounded one of the first rational explanations of the world, according to which the earth was separate from the sky. Anaximander and Anaximenes, both also natives of Miletus on the coast of Asia Minor, put forward different ideas, which nevertheless derived from the same rationale: they proposed the existence of cosmological systems, explained natural phenomena in terms of a small number of “elements”, and invented new concepts – Anaximander’s “equilibrium” and Anaximenes’ “compression” – which can be regarded as the first recognition of the force of gravity.
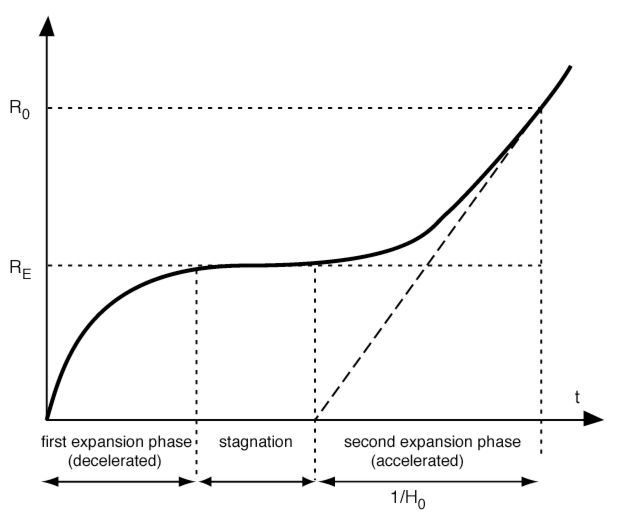
In Lemaître’s so-called “hesitating universe”, a cosmological model he devised in 1931 from Einstein’s field equations, the evolution of the cosmos is divided into three disctinct phases : two periods of rapid expansion are separated by a period of “stagnation”, representing a sort of equilibrium between the forces of gravitational contraction and expansion.
According to Heraclitus of Ephesus, the day was caused by exhalations from the sun, while the night was the result of dark emissions from the earth. The stars and the planets were bowls of fire which, when turned over, gave rise to eclipses and the phases of the moon. The moon itself, pale and cold, moved in the rarefied air above the earth, whereas the sun, our nearest star, was bright and hot.
Meanwhile, the Greeks were amassing measurements which would enable them to plot the stars more accurately. This required specialised instruments – gnomons to measure the sun’s shadow, compasses to fix the positions of the stars in the sky, etc. – as well as a system of notation which anyone could understand (previously the study of astronomy had been restricted to priests): how many fingers’ width above the horizon was such and such a star; where was due north, and so on. As well as mining the extensive archive of observations made by the Egyptians and Babylonians, the Greeks developed their own system of records. The pre-Socratic thinkers refined and analysed the basic ideas of their predecessors from Miletus with the result that the mechanistic view of the world gradually lost currency and a belief in underlying harmony became de rigueur. As early as 450 BC Anaxagoras of Clazomenae was accused of impiety for referring to the sun as a mass of hot metal, to the moon as a second earth and to the stars as burning stones – views no longer considered seemly. Continue reading
