Le satellite Microscope a été lancé, il y a peu, par une fusée Soyouz pour tester le principe d’équivalence. Qu’est-ce que cela et pourquoi vouloir améliorer la précision d’une mise à l’épreuve de cet élément central de la physique déjà fort bien confirmé par de multiples expériences ?
Le principe d’équivalence est le constat suivant : tous les corps chutent de la même manière dans le champ gravitationnel, quelles que soient leurs masses. Il joue donc un rôle central dans la construction de la relativité général car c’est à partir de celui-ci qu’Einstein comprend que, parce que la gravité est la même pour tous, il est peut-être possible de la décrire comme une déformation de l’espace-temps – qui, précisément, nous contient tous – plutôt que comme une force agissant sur les objets.

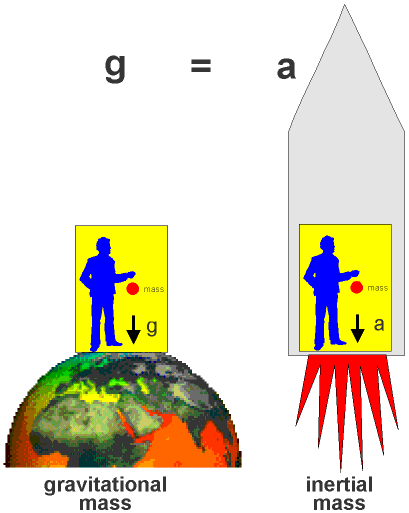
Depuis le XVIème siècle, ce principe a été testé à de multiples reprises et aucune mise en défaut n’a été constatée. La précision atteinte aujourd’hui est de l’ordre de un pour mille milliard ! C’est excellent, le principe est très bien confirmé. Ce qu’il veut finalement dire, c’est que localement (disons dans un volume de taille raisonnable) il est impossible de distinguer le champ gravitationnel d’une accélération. Je suis en ce moment assis sur ma chaise parce que, dit-on, le champ gravitationnel de la Terre m’y contraint (je ne flotte pas dans la pièce). Mais s’il n’y avait plus de gravité et que mon bureau était accéléré vers le haut, je ressentirais exactement la même chose.
C’est l’abandon du champ de gravitation au profit de cette accélération équivalente qui va conduire aux effets subtils de courbure (car l’équivalence n’est que locale) que la relativité générale met en évidence.
Cependant, comme souligné dans cet article, il y a de bonnes raisons théoriques de questionner le principe d’équivalence. Il n’est d’ailleurs pas strictement un principe mais plutôt, dans la formulation actuelle, une conséquence de la première des deux hypothèses de base de la relativité générale. Ces hypothèse sont, d’abord, le couplage universel des champ de matière avec une unique métrique (c’est-à-dire une structure géométrique) et, ensuite, la loi d’évolution de cette métrique. Il faut bien voir que la relativité s’accompagne d’une leçon aux conséquences philosophiques immense : l’invariance de fond. Autrement dit, il n’existe plus de structures absolues et statiques pour décrire l’espace-temps.

Cette diminution du nombre des structures absolues apparaissant dans les théories, au profit d’entités dynamiques ou élastiques n’est pas le seul appanage de la relativité générale et semble être une direction claire de la physique théorique depuis un siècle environ. (Les éventuelles conséquences – fût-ce au sens d’une invitation à la réflexion – dans les champs politiques et ontologiques restent à explorer et je les crois fascinantes …) Or, implicitement, le principe d’équivalence suppose que les constantes de couplage (les paramètres fondamentaux de la physique) sont non dynamiques ! Il induit donc une tension ou une asymétrie entre le caractère évolutif de la structure même de l’espace-temps, qui est le coeur de la relativité générale, et cette rigidité des autres paramètres.
Il y a une cinquantaine d’année, Dicke a en effet montré que si les constantes de couplage variaient spatialement, autrement dit étaient dynamiques, alors des corps de compositions différentes devraient tomber différemment et donc violer le principe d’équivalence. En ce sens, avec une certaine ironie, on pourrait donc dire que la relativité générale, née du principe d’équivalence, suggère en fait l’éventualité d’une remise en cause de celui-ci !
La théorie des cordes prédit un tel comportement dynamique des constantes mais une violation du principe d’équivalence ne serait pas pour autant une « preuve » de la théorie des cordes, ni même une indication très forte en ce sens. Mais ce serait sans aucun doute un signe très excitant de « nouvelle physique ».
Autant de bonnes raisons de suivre les mesures du satellite Microscope.

Qu’est ce qui va changer dans la RG, si cette différence entre masse grave et masse inerte se révèle être bien vraie ?
A mon sens, ça change tout ! (et Aurélien me corrigera si besoin)
En effet, la RG est construite sur l’observation du principe d’équivalence, qui est pris comme un postulat de base. Tout l’édifice intellectuel est construit avec ce postulat (et quelques autres, dont l’invariance de la vitesse de la lumière) : si ce postulat est faux (ou “pas totalement exact” devrais-je dire, car à ~10^-14 près, c’est quand même “presque vrai”), alors toute la construction est fausse/inexacte. Donc ça change tout.
Après, la RG restera vraisemblablement(*) “presque vraie” sur une large gamme de tests, mais elle ne sera plus qu’une approximation d’une théorie plus large qui sera à construire dans certains cas. De même que la mécanique newtonienne n’est qu’une approximation de la RG, la RG ne serait qu’une approximation de cette nouvelle théorie.
(*) Une digression : je garde un doute raisonnable sur la RG en champ faible, en lien avec la matière noire nécessaire dans le modèle cosmologique standard (LCDM). Ce modèle cosmologique part du postulat que la RG est valide à l’échelle de l’Univers et cela nécessite la présence de matière noire (et d’énergie noire, déjà prévue par la RG avec la constante cosmologique ). Mais cette matière noire n’a toujours pas été identifiée et le modèle LCDM explique par ailleurs mal la structure des galaxies et les phénomènes étonnants que l’on observe quand les champs gravitationnels sont faibles (en-dessous de ~10^-10m.s^-2), avec entre autres la “Baryonic Tully-Fisher Relation” (BTFR) : avec la BTFR, la seule mesure de la masse de matière visible (étoiles + gaz) d’une galaxie suffit à expliquer précisément la vitesse de rotation de ses étoiles, alors que dans le paradigme LCDM, masse visible et matière noire ne devrait pas être directement corrélés, et donc pour une masse visible donnée, la vitesse de rotation devrait dépendre de la matière noire réellement présente (et relativement aléatoire) : ce n’est manifestement pas la cas, la BTFR démontre le contraire !
Et … il existe une alternative : ce serait de modifier la gravité en champ faible pour se passer de l’hypothétique matière noire, ce que fait l’approche MOND (MOdified Newtonian Dynamics) et ses extensions relativistes. Concrètement, en appliquant la “recette” MOND à la masse visible d’une galaxie, on prédit une vitesse de rotation des étoiles, prédiction déterministe ET compatible (aux erreurs de mesure près) à ce que l’on mesure et ce, sans recourir à une mystérieuse matière noire présente en quantité ad-hoc et opportune ! Donc contrairement à l’approche LCDM, MOND permet de faire des prédictions sur la vitesse de rotation des galaxies sur la base de leur seule masse visible, et ces prédictions sont celles de la BTFR, et elles sont vérifiées (aux erreurs de mesure près). MOND reste une “recette de cuisine”, mais elle marche redoutablement bien : n’est-ce qu’une recette, ou y a-t-il une “vraie” réalité physique derrière, c’est toute la question …
Et si c’est le cas, la RG serait alors totalement erronée (facteur 2 ou plus) en champ faible. Je n’ai pas vu d’articles de recherche sur le sujet, mais à mon sens les résultats du satellite Gaia devrait nous ouvrir les yeux sur ce sujet dans les années qui viennent (pour confirmer la RG ou, au contraire, renforcer la piste d’une approche de type MOND !). A suivre, mais c’est une autre piste de “nouvelle physique”.
Aurélien, as-tu un avis sur la question 😉 ? (et je serais ravis d’échanger sur le sujet, sur lequel je me suis penché assez en détails)
Bonjour K, Vous prétendez qu’il n’y a pas de preuves observationnelles de la matière noire (non baryonique) ?
On ne fait qu’en accumuler ! Et on décèle maintenant son
influence sous une forme froide et non chaude, c’est à dire qu’elle ne pourrai peut être pas former des assemblages complexes à l’image de la matière baryonique (nous), et elle a même sans douté été le catalyseur de la formation des pré galaxies telles qu’on les voit dans la passé comme des quasars.
Bien cordialement.
Bonjour
Commentaire à ne PAS publier svp : j’ai écrit un long commentaire jeudi ou vendredi dernier, mais il n’est pas visible sur le forum. Est-il problématique (par exemple faux sur ma proposition de réponse) ou va-t-il être publié svp ? Je peux notamment le faire plus court si vous le souhaitez (en supprimant la 2è partie exemple).
Merci beaucoup, cordialement
NGC 1365
Bonjour
Que serai-je sans les 4 dimensions, sans le contact de ces interprétations, à l’égard de mon égo, je la trouve ci belle, elle vole dans l’espace de mon lieu je la frôle juste un instant pour quel disparaisse.
Jacques
Bonjour à tous; (svp excusez parfois les “non-accents” je suis en QWERTY)
NB: Je ne suis pas du tout compétent sur le plan scientifique et mes questions ou remarques sont plus d’ordre intuitif.
La RG et sont principe d’équivalence, ne peuvent-ils pas être considérés comme parfaits jusqu’a un certain point référentiel, tout comme l’était la théorie de Newton à son époque?
En effet, jadis, bien que révolutionnaire, et pour cause, la théorie de Newton laissait apparaitre quelques imperfections mineures (Ex : le calcul de l’orbite de Mercure), mais le bon en avant et les outils de mesure disponibles ne permettaient quasiment pas de remettre en cause la théorie.
La RG peut-elle être perçue de telle sorte qu’elle fonctionne quasiment parfaitement en relation avec son temps, le bon scientifique apporté, et la precision des outils de mesure du XXeme siècle ?
Intuitivement ou instinctivement, je me laisse influencer par l’idée que, aussi infinitésimale que soit la chose, lorsque je pose le pied par terre, la Terre est également attirée vers moi, tout comme je le suis par elle. Par consequent, j’en conclus hâtivement qu’une boule d’une masse N fois supérieure a une boule de pétanque par exemple, tombe en effet un peu plus vite vers la Terre, et que cette dernière sera plus attirée vers cette boule plus lourde.
Cette intuition est-elle à ce jour totalement erronée? Ou simplement les ordres de grandeur mis en jeu sont-ils si insignifiants que nous ne sommes pas en mesure pour le moment de l’experimenter correctement?
Cordialement
Alexandre
Alexandre, vous avez raison mais la correction est en 1+m/M, avec M la masse de la terre (6.10^24 kg …).
On prend 1 dans le calcul simple, et avec une boule de 1 kg, l’erreur est de 1 / 6.10^24, donc nettement inférieure à 10^-24 : non mesurable !
Même avec 1 milliard de tonnes, erreur inférieure à 10^-12 : très difficilement mesurable (et pas simple à mener comme expérience ; -). Sans compter qu’avec ces précisions extrêmes, la théorie newtonienne est insuffisante et il faut prendre en compte la Relativité Générale pour obtenir des résultats précis, tout comme la forme détaillée de la Terre, qui n’est ni ronde ni homogène … Bref, non mesurable.
Mais dans l’absolu, vous avez raison, deux corps de poids différents chutent à des vitesses (très très) légèrement différentes sur Terre, car eux mêmes créent des champs gravitationnels (différents, car de poids différents).
Ce que je n’ai jamais compris dans la RG telle qu’exposée actuellement : on n’a pas attendu Einstein pour montrer que g = a. Avec notre éducation du 20è siècle, on apprend tous, dès la classe de 2nde, que la masse pesante est la masse inertielle, grâce à Newton (ce n’était peut-être pas évident avant le 20è siècle). La pesanteur est une accélération, et (sans la résistance de l’air), tous les corps chutent avec la même accélération, quelle que soit leur masse. (Un peu comme pour l’éther, on a du mal à se mettre dans la peau de quelqu’un du début du siècle, qui n’arrivait pas à penser que la lumière pouvait se propager dans le vide absolu). Donc la RG me passe en partie au-dessus à cause de ça…
Bonjour Eric H,
Ouille, le vide des physicien n’est pas le vide absolu, il est même plein d’énergie.
” Tous les corps chutent de la même manière dans le champ gravitationnel, quelles que soient leurs masses.”
Mais si une fusée A doit faire décoller un satellite de 10 tonnes et qu’une fusée B doit faire décoller un satellite de 30 tonnes, la quantité d’énergie ne sera pas identique pour soulever les masses respectives en regard de la pesanteur égale dans les deux cas: y compris en incluant la différence de masses des fusées en fonction de la masse énergétique moteur + réservoir qui jouent une sorte de compensateur “avant-après” la combustion en parallèle de la règle d’Equivalence.
En effet, si on place les deux satellites au bout d’un ressort générique, il semble que lors de la poussée en accélération au moment du décollage respectif, le satellite B le plus lourd va produire une oscillation mécanique et quantique plus importante que le satellite A: à vitesse de pesanteur égale; depuis le champ terrestre et donc durant la vitesse d’éjection vers le stade de l’apesanteur autour de la Terre.
Dans ce cas, est-ce que le principe d’Equivalence est vraiment pertinent? Où répond-il en quelque sorte à côté? ou insuffisamment? Ou trop rapidement comme une équivalence pesanteur-gravitation??
N’est-ce pas une problématique plus démonstratrice que les jumeaux A et B de Langevin en ce qui concerne la condition humaine avec son rapport terrestre-cosmos?
N’est-ce pas une erreur de la Relativité qui justement empêche les chercheurs de pouvoir l’appliquer en tous domaines?
Est-ce que l’Enthalpie atmosphérique n’est pas galvaudée au profit de l’Entropie cosmologique? à ne chercher que l’isolation du vide sans prendre en compte l’utilité de l’échange énergétique de la pression atmosphérique?
Ne peut-on pas donner une probabilité concernant le principe d’Equivalence qui interpelle le lecteur vulgaire? Erreur?? ou pas Erreur?
Enfin, si on reproduit la même expérience de décollage A et B depuis une plate-forme spatiale en apesanteur, cette seconde expérience de pensée de révèle-t-elle pas par défaut les hypothétiques manquements du principe d’Equivalence?
Est-ce que vous pouvez donner une explication?
Merci pour la réponse.
Merci pour vos explications et pour vos livres.
La réponse du problème complexe des deux fusées A et B qui font faces au principe d’Equivalence pesanteur-gravitation ne se trouve-t-elle pas au bout du ressort générique? Et respectif?
Je donne ma réponse sans être spécialiste.
On aborde l’expérience de pensée sous trois versions:
la première consiste à suspendre les satellites A et B depuis un ressort générique de section identique.
>La Fusée A EamC² est prévue pour faire décoller la charge satellite A de 10 tonnes.
>La fusée B EbmC² est prévue pour faire décoller la charge satellite B de 30 tonnes.
Le ressort de section A est égal au ressort de section B: l’oscillation constatée lors de l’accélération hrôg et v² laisse présager que l’amplitude des deux ressorts sera contrainte pour la masse la plus légère et idéale pour la plus lourde, car ne l’oublions pas, l’expérience de portage sous ressort doit résister à l’oscillation des masses, et donc de la plus lourde: on se place dans une relation parallèle du ‘qui peut le plus, peut le moins’.
L’ utilisation parallèle et respective du ressort générique sert à transformer l’intensité de la pesanteur issue à la fois de la contre-poussée et du champ de la gravitation: en quelque sorte, un observateur voit passer au sein du ressort, la transformation sous forme d’une hélicité entre la position terrestre et la position Espace.
On parle donc également d’une relation espace-temps héliocentrique, puisque le transfert compensatoire pesanteur-gravitation permet le voyage d’éjection terrestre du sol vers les étoiles.
La seconde version consiste à modifier uniquement la section du ressort: celui-ci est adapté en fonction de la charge respective des satellites A et B. On constatera alors que lors de l’accélération non-constante et compensatoire complexe, les satellites vont exercer une oscillation mécanique respective: jusqu’à stabilisation? Et bien non! Puisque si la fusée sort complètement du champ de pesanteur terrestre,
le mouvement mis en oscillation devrait conserver sa période d’oscillation à l’infini ( en fait c’est impossible: il va la perdre au moment d’une inversion pesanteur-gravitation. D’où la différence entre gravité de force: et inertie tangentielle de la gravitation.)
Dans ce cas, on ne peut pas aussi rapidement affirmer une équivalence entre pesanteur et gravitation.
La troisième version consiste à placer un ressort spécifique pour chaque charge satellite A et B, et prétendre en fait à une fusée à poussée unique: une expérience sur deux sera un échec au décollage. Pourquoi? et notamment lorsque la poussée générique E=mC² sera inférieure à la masse du satellite le plus lourd. On se retrouve à nouveau dans une relation du ‘qui peut le plus, peut le moins’.
De ce fait, on en conclue qu’on ne peut attribuer le principe d’Equivalence que pour une amplitude stricte de forme et non pas à une certitude de fond: d’où justement la corrélation avec l’idée de courbure espace-temps et donc de prise de forme du champ cosmologique. Mais jamais de fond!
D’où peut donc provenir le fond idéal de l’Equivalence?
Il est avant tout relatif à notre propriété d’observation, et donc à l’aspect cognitif. Par conséquent, notre place humaine d’observateur également spécifique au facteur d’échange avec le milieu atmosphérique, tient compte de l’enthalpie avec ce milieu.
En d’autres termes, Albert Einstein oublie de démontrer que l’acteur dans le wagon peut uniquement se contenter de tenir la balle en l’air et qu’il exerce déjà une équivalence intermédiaire directe dans l’expérience de pensée avec l’observateur situé sur le quai de la Gare.
D’autre part, si tous les objets restent en suspensions dans l’ascenseur en chute libre, on pourra aussi constater qu’en allumant la pipe d’Albert Einstein, la fumée monte dans le sens opposé.
Enfin si on complémente l’expérience de l’ascenseur et de la pipe avec une lanterne thaïlandaise, celle-ci monte en mouvement “co-axial” et opposé par rapport au mouvement de chute contraire de l’ascenseur d’Albert Einstein.
Dans ce cas, pour compenser la chute, la lanterne utilise de l’énergie E=mC² qui doit donc venir se soustraire comme une équivalence transitoire entre la pesanteur et la gravitation générale “outre-sphère”: on en conclue donc qu’au départ, on parle de force inter-réduite, et qu’ensuite on parlera de champ courbe.
On entre alors dans une interprétation Newton-Einstein unifiée!
Je vous souhaite bon courage si vous souhaitez résoudre cette expérience de pensée: je pense qu’elle en vaut le détour si elle n’a jamais été étudiée dans le cadre de l’astrophysique ou de l’aérospatiale.
Bon courage et merci pour la future réponse.
Let’s go! And peace of around the world!! Nice to meet you! Allo!! Allo!!! I’am en extra-terrestre! And you! Where do you come from?? Tera plane??? Or Galaxy Gala! So! Sorry to disturb you in your physician mind! You know what?? I’am happy: I’ve found the universal Einstein formulation: E [différent de ] m C Rond. Good travel in the time. I just accross the space-time! Ciao!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Speed so quickly!!! Sorry! My english galactic is no good! E [ différent ] de m C Rond!!! Ow!!!Owwww!!!! OW!!!!!!!!
Le plus grand des mépris n’a de compte que dans l’homme sans intelligence! Il ne saurait faire décoller du vide sinon qu’il le transporte comme un fardeau dans l’éternité aveugle et sourde!
Vérifier le principe d’équivalence?? ça a l’air assez simple!
Le satellite qui flotte en apesanteur dans l’Espace sur la photo semble vérifier par lui-même le principe d’équivalence: il n’a besoin de rien d’autre! semble-t-il! N’est-ce pas ???
Le principe d’équivalence est faux: où plutôt trop conduit dans un archétype relativiste selon Einstein…
On ne peut pas faire correspondre deux influences différentes ( pesanteur et apesanteur ) pour satisfaire la loi de la gravitation générale.
Einstein s’amuse à une sorte d’ordre anti-quantique: la forme qui existe sous le produit d’une chute à un instant ne peut pas exister “en même temps” comme le dividende d’un facteur vide gravitationnel ailleurs dans l’Espace.
On se demande quelle hybridation cherche Einstein: quelle équivalence entre l’inspir et l’expir par exemple?? Un et aucun: la réponse se trouve autrement! C’est certain!!!
Tout le reste n’est que chimère accordéoniste: la Physique du 21ème siècle devrait reprendre ses postulats. Elle n’arrivera jamais à universaliser la grande équation de tous les temps.
Petite astuce: la Terre tend à réduire le mouvement sur elle-même tout en tournant autour du Soleil!
Il semblerait qu’il y aie quelque chose à comprendre de nouveau!
Composition of the vector : Free fall
Vector of gravity and inertial force is possible to compose. It seems to show that the two are inviolable and non-interference each other (it will be the same on two gravity). It will be the same also on vector of gravity and inertial force that act at an optional point of an elevator cabin in free fall.
Sorry, I cannot receive E-mail. I do not have PC.
http://www.geocities.co.jp/Technopolis/2561/eng.html
Les Univers parallèles ne sont il que de la fiction ou peuvent il vraiment exister?