The thought experiments which have been described in my previous post Back to the basics are more than an intellectual exercise, because if black holes really exist (and we have strong observational arguments to believe that), then there is a good chance that they will be illuminated by a natural light source. For a black hole or a planet the most obvious form of lighting is a star. This star could, for example, be bound to the black hole in a binary system. Although such systems are common throughout our Galaxy, the corresponding black holes would be impossible to detect by this effect, as their image by reflected light would be drowned in the intense light of the direct image of the star itself.
A much more interesting situation from an observational point of view is when the source of light comes from a series of rings of matter in orbit around the black hole. It is believed that a number of black holes are surrounded by such structures, which are called accretion disks. Saturn’s rings are an excellent example of an accretion disk; they consist of amalgamated pieces of rock and ice which reflect the light of the distant Sun, whereas those of a black hole consist of hot gas brighting by itself (another important difference is that the accretion disk of a black hole is continually being supplied with gas, whereas that surrounding Saturn is the remnant of the primordial Solar System).

The gases fall slowly into the black hole, like water in a whirlpool. As the gas falls towards the black hole it becomes hotter and hotter and begins to emit radiation. This is a good source of light: the accretion rings shine and illuminate the central black hole. One can then ask : what would be the apparent image of the black hole accretion disk ?
 I was the first to solve the question in an article published in 1979 in the specialized journal Astronomy and Astrophysics (it can be uploaded here). Here is a funny anecdote : several years later, I was told that some readers who discovered my simulated picture of a black hole surrounded by a luminous disk believed that the mysterious author of the article used the name Luminet as a pseudonym !
I was the first to solve the question in an article published in 1979 in the specialized journal Astronomy and Astrophysics (it can be uploaded here). Here is a funny anecdote : several years later, I was told that some readers who discovered my simulated picture of a black hole surrounded by a luminous disk believed that the mysterious author of the article used the name Luminet as a pseudonym !
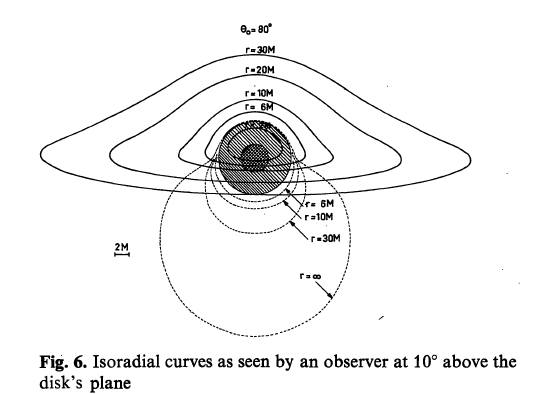
Figure below shows the contours of a circular disk surrounding a spherical black hole. The image is taken on a photographic plate at a great distance, in a direction which is inclined by 10° above the plane of the disk. The strong curvature of space-time near the hole manifests itself as a distortion of the apparent image of the disk. In the case of Saturn’s rings, this is reduced to a series of ellipses because they are seen through a practically flat space-time. But here, the image is split into two. The primary image is formed by light rays emitted from the upper side of the disk, and deviated by less than 180°. The first surprise is that all of the upper side of the ring in front and behind the black hole is visible, including the portion which would “normally” be hidden in an uncurved geometry (Saturn’s rings observed from the Earth are partially hidden by the planet’s disk). Even more surprising is that the curvature of space-time around the black hole enables us to observe the lower side of the rings. This is the secondary image. So it is possible to observe both the upper and lower sides of the accretion disk !
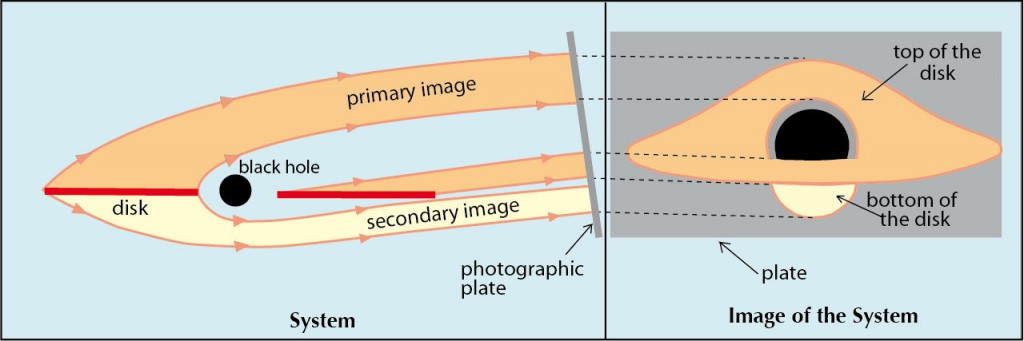
Much more precisely, figure 6 from my 1979 article depicts the isoradial curves (i.e. at constant radial distance from the black hole) of a thin disk around a spherical black hole, as they would be seen by an observer at 10° above the disk’s plane. In ordinary Euclidean flat space they would be simple ellipses, but in the curved geometry of the black hole, they take distorted shapes that I could calculate by integrating the equations of light ray trajectories in Schwarzschild space-time .
In fact there is an infinity of images, because the light rays emitted by the disk can travel any number of times around the black hole before escaping from its gravitational field and being observed by a distant astronomer. The primary image shows the upper side and the secondary image shows the lower side, the third image shows the upper side again, and so on. However, higher order images are not optically interesting because they are stuck to the edge of the central black spot, the latter representing the silhouette of the actual black hole expanded by a factor 2.6 .
For comparison, the now infamous image of a black hole accretion disk as shown in the movie Interstellar – resulting from the collaboration between the film’s director Christopher Nolan and the well-known American astrophysicist Kip Thorne – also shows the isoradial curves of the disk, with the differences that in Nolan’s film, the view was calculated for an observer located within the plane of the disk and not above (this explains the symmetry of the image with respect to the equatorial plane), and for a rotating black hole (this last effect having little influence on the resulting image).

Photographing a black hole
These illumination experiments, although idealised, at least show how a black hole, through its gravitational field, acts on radiation as a sort of lens which multiplies images of a single unique source. Let us now consider a more realistic situation. It is not enough to calculate the propagatin of light rays in curved space-time, we must also take account of the physical properties of the accretion disk .
Rings of matter around celestial bodies have been intensively studied over the last decades because they are related to a large number of astronomical phenomena: giant planets (Saturn, Jupiter, Uranus and Neptune), protoplanetary systems, binary star systems where one of the partners is a condensed star (white dwarf, neutron star and black hole), etc. The gravitational field around a black hole sucks in the overflowing gas of its companion, stores it in the accretion disk and slowly consumes it.
Detailed models of accretion disks explain the high energy radiation emitted by some binary star systems such as Cygnus X-1. On a much greater scale, the high luminosity of the nuclei of certain galaxies and quasars can also be explained by the flow of matter into a black hole of several million or several billion solar masses.

In most of the cases, the mass of the accretion disk is negligible compared to the black hole’s mass : then each particle of the disk is in free-fall in the black hole’s gravitational field. Consider the simple case when the particle orbits in the plane of symmetry of the black hole along circular trajectories. The speed of the particle depends on the radial distance to the center of the black hole. As two particles on neighbouring orbits don’t move at the same speed, they interact and generate viscosity which heats the disk. The more the disk is close to the black hole, the more it is hot and bright. Since close to the black hole surface the gravitational field is extremely high, the gas is heated at very high temperatures – typically corresponding to X-ray radiation.
Now, when the flow of matter into a black hole is not too great, it forms a very thin accretion disk. In that case, the proper luminosity of the disk can be accurately calculated, according to a model provided by Don Page and Kip Thorne in a 1974 reference article : the intensity of radiation emitted at any given point of the disk only depends on its temperature, and the matter only depends on the radial distance to the black hole.
In 1978, I reconstructed the photographic appearance of a spherical black hole surrounded by a very thin gaseous disc, by using a computer to calculate the trajectories of light rays in the Schwarzschild space-time. The image was first published in a popular article in a French magazine (reference: B. Carter & J.-P. Luminet, Les Trous Noirs, Maelströms cosmiques, La Recherche n°94, 944, 1978), before being published a few months later, in English, in the above-mentioned article (J.-P. Luminet : Image of a Spherical Black Hole with Thin Accretion Disk, Astron.Astrophys. 75, 228, 1979) with all the technical explanations.
In a thin disc the intensity of radiation emitted from a given point on the disc depends only on its distance from the black hole. The reconstituted image is therefore universal, that is, it is independent of the mass of the black hole and the flow of gas into it. It could as easily represent a black hole 10 kilometres in diameter or one that was as large as the Solar System and swallowing interstellar gas.
As expected from pure geometrical reasoning, the upper side of the disk is completely visible. However, only a small part of the lower side is observable. In a realistic situation the gaseous disk is opaque; therefore it absorbs the light rays that it intercepts. It follows that a major part of the secondary image – showing the lower side of the disc – is occulted by the primary image; the very deformed visible part is at the edge of the black hole.
No radiation comes from the region between the black hole and the inner edge of the disk. The properties of the Schwarzschild space-time forbid the accretion disk from touching the surface of the black hole. The almost circular orbits of the gas in the disk can be maintained only down to a critical distance of three times the Schwarzschild radius. Below this the disk is unstable; the gas particles plunge directly towards the black hole without having enough time to emit electromagnetic radiation.
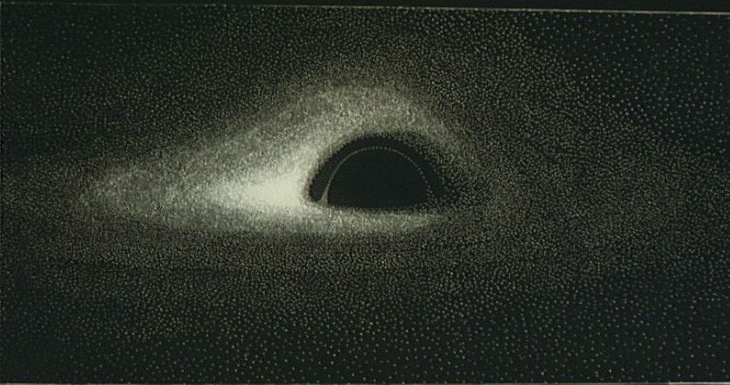
The main characteristic of a “photograph” of a black hole is the apparent difference in luminosity between the different regions of the disk. The maximum brilliance comes from the inner regions closest to the horizon, because it is here that the gas is hottest. However, the apparent luminosity of the disk (as recorded for instance by a camera embarked on a spaceship) is very different from the intrinsic luminosity (as it would perceived by an observer comoving with the disk’s particles).
Apart from the geometric distortion of the circular rings, the radiation picked up at a great distance by a photographic plate is frequency- and intensity-shifted with respect to the emitted radiation. There are two sorts of shift effects. There is the Einstein effect, in which the gravitational field lowers the frequency and decreases the intensity. It is important only near the event horizon and is independent on the observer’s position.
In addition there is the better known Doppler effect, where the displacement of the source with respect to the observer causes amplification as the source approaches (a blueshift) and attenuation as the source retreats (a redshift).
The combination of the two effects (Einstein and Doppler) is not trivial. In my 1979 article I calculated it at each point of the photograhpic plate. The figure below depicts the curves of constant spectral shift, as seen by an observer at 10° above the plane of the disk.
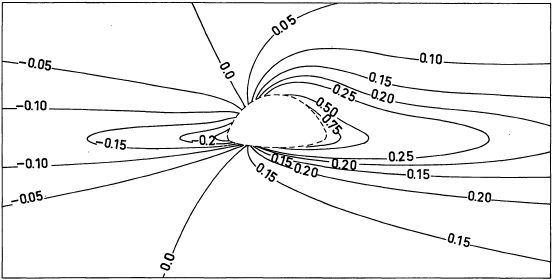
In our case the Doppler effect dominates, and it is caused by the disk rotating around the black hole. The regions of the disk closest to the black hole rotate at a velocity approaching that of light, so that the Doppler shift is considerable. The sense of the rotation of the disk is such that matter recedes from the observer on the right-hand side of the photograph and approaches on the left-hand side. As the matter recedes, the Doppler deceleration is added to the gravitational deceleration, explaining the very strong attenuation on the right-hand side. In contrast, on the left-hand side the two effects tend to cancel each other out, so the image more or less retains its intrinsic intensity.
In order to obtain the final photograph, we must therefore correct the intrisic luminosity of the disk by the spectral shift effects, which amplify or attenuate the apparent luminosity received by a distant observer. Figure below, from my 1979 article, depicts the curves of constant apparent luminosity as seen by an observer at 10° above the plane of the disk.
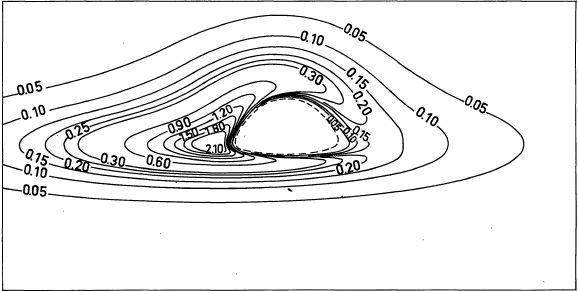
The final black and white “photographic” image was obtained from this pattern.
In a next post I’ll show how, after my pioneering article, many searchers used more powerful computers to introduce colors and motion, and get more and more realistic visualizations of black hole accretion disks – until the latest calculations, by Thorne and the team of visual effects of the movie Interstellar, just published in Classical and Quantum Gravity.

I think it would be awesome to make some prints of the original black hole simulation graph. Is there a high resolution version of the simulation available?
Yes! I’ve searched but never found one. Would be so amazing g to find a print!
Really good and clearly written posts (from a non-physicist’s viewpoint). thanks!