The centre of the black hearth,
of setting suns on the shore :
ah ! well of magic
Arthur Rimbaud (Illuminations)

As probably all of you already know, the Interstellar movie tells the adventures of a group of explorers who use a wormhole to cross intergalactic distances and find potentially habitable exoplanets to colonize. For the scientific part, the film director, Christopher Nolan,  has collaborated with a colleague of mine, the famous physicist Kip Thorne, a specialist in general relativity and black hole theory.

With such a scientific consultant, the promotion of the movie insisted a lot on the realism of the black hole images calculated by Kip Thorne and the team of visual effects company Double Negative. The most striking one shows a glowing accretion disk appearing above, below  and in front of the black hole.

As soon as the movie was displayed on the screens, a lot of physics blogs have commented in details the “Science of Interstellar”. Kip Thorne himself has published a such entitled popular book, to explain how he tried to respect scientific accuracy despite the sometimes odd demands of Christopher Nolan, ensuring in particular that the depictions of black holes and relativistic effects were as accurate as possible.

Since, as soon as 1979, I was the first researcher to perfom numerical calculations and publish the simulated image of a black hole surrounded by a thin accretion disk (you can upload the technical article here), to inaugurate this new blog I’ll devote a series of 3 posts to the basics of black hole imaging. A good part is adapted from a chapter of one of my books, published in French in 2006, Le destin de l’univers – unfortunately not yet available in English.

Can a black hole be visualized ?

One of the best ways of representing a body is by its image, by photographing or filming it. It seems impossible to photograph or to film a black hole, since no material, not even light, can escape it. The black hole is a priori perfectly invisible. However, it is not necessary that an object emits light so that we can perceive it ; we can also illuminate it in a way that it sends back the light which it received. Planets, whose cores do not generate thermonuclear energy, would remain optically invisible if their surface did not reflect the Sun’s light.

What is true for a planet is also true for a black hole. We shall see certainly nothing in the absence of any light source, but a suitably illuminated black hole is capable of sending back an image, thanks to the particular paths followed by the light rays emitted in its surroundings.

So photographed under spotlights, the black holes, which are not holes but regions of space-time with specific physical properties, are not either really black.

A matter of lightening

Every natural body absorbs and reflects electromagnetic radiation in some way. The thought experiment illustrated in the figures below uses a parallel beam of light to illuminate various species of spherical and ideal bodies, and to observe the reflected light in a direction orthogonal to the incident one. The type of image received depends on the nature of the body and how it reacts to electromagnetic radiation.

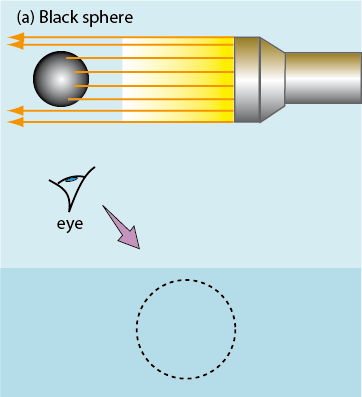In the case of a perfectly black body (for example a sphere covered with perfectly absorbing black paint) all the light rays are absorbed, and in the absence of any reflection the observer will see absolutely nothing of the sphere.

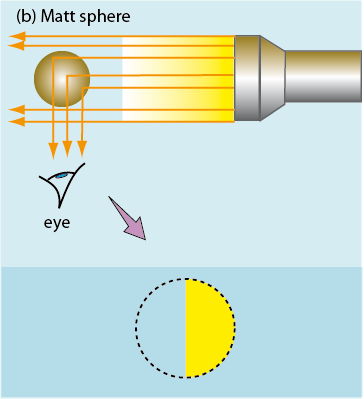In the case of a matt surface (such as the Moon and the planets), the light is ‘isotropically’ reflected, that is, with the same intensity in all directions. Consequently at each point on the surface a single light ray may be deviated exactly 90° with respect to the incident direction and reach the observer. The result shows the familiar image of the half Moon.

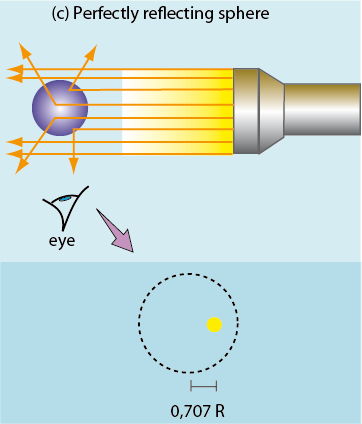The third example concerns a perfectly reflecting metallic sphere. This time a single point on the surface deviates an incident light ray by 90° and sends it to the observer. The image of the sphere is reduced to a unique spot of light, situated at a distance of √2/2 ≈ 0.707 times the real radius of the sphere.

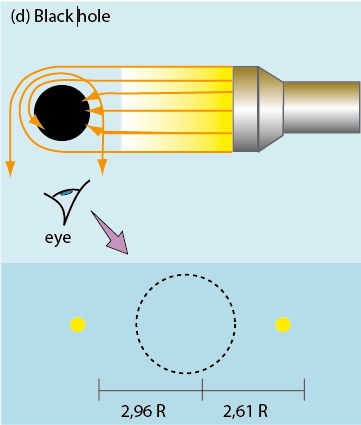The final case is that of a black hole of mass M, here assumed to be non-rotating, thus described by the Schwarzschild geometry. The essential difference from the preceding examples is that a black hole has not a tangible hard surface against which light rays can strike and be reflected. It is the black hole’s gravitational field which deviates the light rays. The black hole’s sphere of influence is not therefore a single sphere – the event horizon – but extends to infinity. The trajectories of light rays are not altered by the impact with a surface, but are curved by the gravitational field. In the experiment where it is illuminated, the black hole’s gravitational field deviates several light rays towards the observer. The image of the black hole consists of a series of illuminated spots. On the left, at 2.96 times the Schwarzschild radius of the black hole (equal to 2M), the ‘primary’ image is produced by light rays which have been deviated by 90°. On the right, at 2.61 times the Schwarzschild radius the ‘secondary’ image is produced by light rays which have been deviated through another half circle (a total of 270°). The complete calculation of the geodesics of the Schwarzschild space-time corresponding to the light ray trajectories shows that there is an infinity of images; the third one corresponds to light which has been deviated by 450°, and so on adding a half turn each time. However, in practice, the images of order higher than two have such a low intensity and are so close to the primary and secondary images that they cannot be resolved.

We can therefore conclude that among the various celestial bodies which are not intrinsically bright, black holes are far from being the darkest. They are easier to detect than a black painted sphere or a highly reflective sphere!

The black hole in glory

A variant on the preceding experiment consists of illuminating a black hole and observing the light reflected back in the same direction. The result is shown here.

The image of the actual black hole is magnified to 3√3/2 ≈ 2.6 times its real diameter. This is because a large part of the incident beam is captured by the black hole: not just the radiation which directly strikes the event horizon but also that which passes within 5.2M of the centre (the true radius of the black hole being equal to 2M). The black disk appears to be surrounded by a series of concentric light rings. The external ring, at radius 5.34 M, is produced by light rays deviated by 180°, the inner rings by light rays deviated by additional turns. The final result is like the glory effect, well-known in traditional optics: when sunlight is scattered by innumerable water droplets in mist, it is sometimes possible to see in reflection the shadow of one’s own head surrounded by brilliant rings of light centred on the line of sight.

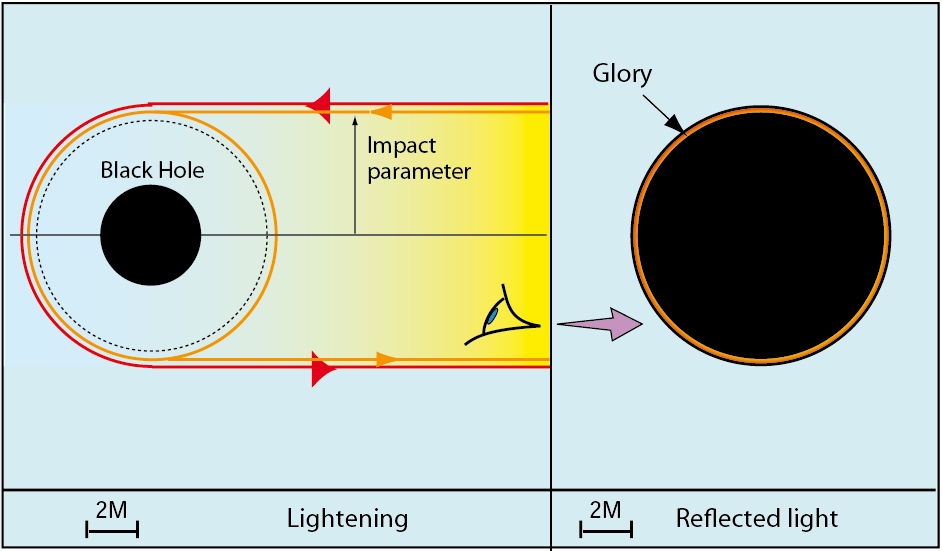In the case of black holes with a glory effect, only the outer ring would be visible, as it is not possible to resolve the rings of higher orders. This is not only a matter of brightness, but also a matter of resolution.

In  2002,  David Holz and John Wheeler have suggested that the primary ring could be detectable in the case of a stellar mass black hole located at the border of our solar system and reflecting the light of our star, the Sun. John Wheeler (who coined the terms of black hole and wormhole) entitled the article  “Retro-MACHO : pi in the sky”, meaning both that isolated stellar mass black holes belonged to the category of Massive Astrophysical Compact Halo Objects, a candidate for baryonic dark matter, and their detectability thanks to the deflection of light by the “magic angle” 180°.

All during his long life, John Wheeler liked putting forward non conventional ideas which, for the greater part, showed themselves very fruitful. This last proposal has however few chances to become a reality one day. The calculation of the return of light indeed involves a 10 solar masses black hole situated at less than 3 light years from us, the magnitude of the “glorious ring” would not exceed 32 in the most favorable case, that is 100 times lower than the magnitude of the weakest object until then detected by the most powerful telescopes. Besides, it is estimated that the average density of  stellar mass black holes in our region of the Milky Way is of the order of 0.00001 per cubic light year. It would thus be extraordinarily improbable that a stellar black hole is so close to  us.  Consider nevertheless the hypothesis, namely a 1 M_S black hole located at only 1,5 light year. The calculation gives that the associated “retro-macho” would have magnitude 43, i.e. a luminosity 100 000 times weaker than the faintest object ever detected!

Optics in curved space-time

The curvature of light rays is a fundamental characteristics of the theory of general relativity, according to which the propagation of light depends on gravitational fields. The Universe is described as a 4-dimensional space-time, a kind of flexible and elastic fabric distorted by the gravitation – that is the massive bodies which it contains. Forming the weft of this fabric, the paths of light are like threads cast on abysses. Just like the matter, the energy generates a gravitational field (since matter and energy are equivalent, linked by the famous formula E = mc²) ; conversely, matter and energy undergo the effects of gravity. In particular, massless particles in motion, such as the quanta of light called photons, have an energy (given by their frequency) : their trajectories are thus modified by gravity. The more the gravitational field is intense, the more the trajectories of light rays that cross it are deflected. In an excellent approximation which means neglecting the influence of the proper gravitational field of the photons compared to that of the black hole, the light ray followed by each photon strictly follows a geodesic of space-time, that is the line of shortest length between two points. Geodesics are the equivalent of straight lines in flat space-time, and they weave the shape of curved space-time.

The gravitational field of a black hole strongly distorts the spacetime in its neighborhood. Below a given distance to its centre, which defines the (immaterial) surface of the black hole called event horizon, no particle (massless or not) can escape. Outside the event horizon, light rays can escape, but the strong curvature of space-time considerably modify their trajectories.

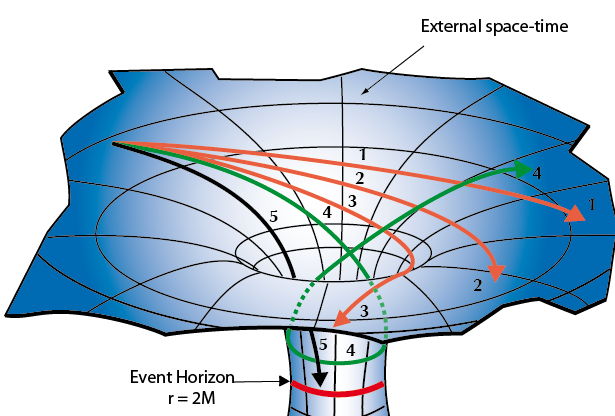
We can trust the equations of general relativity to calculate the propagation of light rays in the neighborhood of black holes. The calculation requires a preliminary mathematical analysis, followed by a numerical integration on the computer. By this method we can obtain the images of a black hole illuminated by any kind of light sources distributed by any way.

We shall do this in the next post.