Monthly Archives: January 2016

Cinema, Sciences

The Warped Science of Interstellar (5/6) : Time machine and Fifth Dimension

2 Comments

Sequel of the preceding post The Warped Science of Interstellar (4/6)

In november  2014, the Hollywood blockbuster and science-fiction movie Interstellar was released on screens and  much mediatic excitation arose about it.
This is the fifth of a series of 6 posts devoted to the analysis of some of the scientific aspects of the film, adapted from a paper I published last spring in Inference : International Review of Science.

TIME TRAVEL INSIDE GARGANTUA

Interstellar-FLprStills16-2nd-Batch

In the last part of the film, the main character, Cooper, plunges into Gargantua. There, beware the tidal forces breaking anything up ! Indeed in the Schwarzschild geometry, the tidal forces become infinite as r -> 0 ; so, even for a supermassive black hole like Gargantua, once past safely the event horizon and approaching the central singularity, everything will be ultimately destroyed. Happily for the continuation of the story, Gargantua has a high spin, and its lethal singularity has the shape of an avoidable ring. Thus the space-time structure allows Cooper to use the Kerr black hole as a wormhole ; he avoids the ring singularity and transports to another region of space-time. In the movie he ends up in a five-dimensional universe, in which he will be able to go backwards in time and communicate with his daughter by means of gravitational signals.

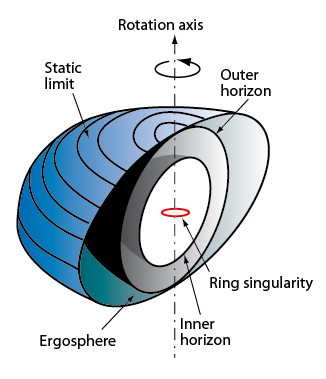
Inner structure of a rotating black hole with a ring singularity
Inner structure of a rotating black hole with a ring singularity

A lot of research has been done on whether the laws of physics permit travel back in time or not. Black hole physics gives interesting results but no firm answers. As seen in the post The Warped Science of Interstellar (1/6), according to Penrose-Carter diagrams a rotating black hole could connect myriads of wormholes to different parts of the space-time geometry. Since two events can differ in time as well as in space, it would be possible to pass from one given position at a given time, along a carefully chosen trajectory, through a wormhole, and arrive at the same position but at a different time, in the past or future. In other words, the black hole could be a sort of time travel machine.

Noneless a journey back through time is an affront to common sense. It is difficult to accept that a man could travel back through time and kill his grandfather before he has had the time to produce children. For the murderer could not have been born, and could not have murdered him, and so on… Such time paradoxes have been pleasantly presented in the celebrated series of movies Back to the future.

Continue reading →

Cinema, My books & articles, Sciences

The Warped Science of Interstellar (4/6) : Time dilation and Penrose process

10 Comments

Sequel of the preceding post The Warped Science of Interstellar (3/6)

In november  2014, the Hollywood blockbuster and science-fiction movie Interstellar was released on screens and  much mediatic excitation arose about it.
This is the fourth of a series of 6 posts devoted to the analysis of some of the scientific aspects of the film, adapted from a paper I published last spring in Inference : International Review of Science.

A HUGE TIME DILATION

The elasticity of time is a major consequence of relativity theory, according to which time runs differently for two observers with a relative acceleration – or, from the Equivalence Principle, moving in gravitational fields of different intensities. This well-known phenomenon, checked experimentally to high accuracy, is called « time dilation ».

The celebrated "smooth watches" by Salvador Dali are a nice metaphor of time elasticity predicted by Einstein's relativity theory.
The celebrated “smooth watches” by Salvador Dali are a nice metaphor of time elasticity predicted by Einstein’s relativity theory.

Thus, close to the event horizon of a black hole, where the gravitational field is huge, time dilation is also huge, because the clocks will be strongly slowed down compared to farther clocks. This is one of the most stunning elements of the scenario of Interstellar : on the water planet so close to Gargantua, it is claimed that 1 hour in the planet’s reference frame corresponds to 7 years in an observer’s reference frame far from the black hole (for instance on Earth). This corresponds to a time dilation factor of 60,000. Although the time dilation tends to infinity when a clock tends to the event horizon (this is precisely why no signal can leave it to reach any external observer), at first sight a time dilation as large as 60,000 seems impossible for a planet orbiting the black hole on a stable orbit.

As explained by Thorne in his popular book, such a large time dilation was a « non-negotiable » request of the film director, for the needs of the story. Intuitively, even an expert in general relativity would estimate impossible to reconcile an enormous time differential with a planet skimming up the event horizon and safely enduring the correspondingly enormous gravitational forces. However Thorne did a few hours of calculations and came to the conclusion that in fact it was marginally possible (although very unlikely). The key point is the black hole’s spin. A rotating black hole, described by the Kerr metric, behaves rather differently from a static one, described by the Schwarzschild metric. The time dilation equation derived from the Kerr metric takes the form:

1 – (dτ/dt)2 = 2GMr/c2rho2, where rho2 = r2 + (J/Mc)2cos2θ.

Continue reading →

Cinema, My books & articles, Sciences

The Warped Science of Interstellar (3/6) : Accretion Disk and Tidal Stress

5 Comments

Sequel of the preceding post The Warped Science of Interstellar (2/6)

In november  2014, the Hollywood blockbuster and science-fiction movie Interstellar was released on screens and  much mediatic excitation arose about it.

This is the third of a series of 6 posts devoted to the analysis of some of the scientific aspects of the film, adapted from a paper I published last spring in Inference : International Review of Science.

VISUALISATION OF THE ACCRETION DISK

Since a black hole causes extreme deformations of spacetime, it also creates the strongest possible deflections of light rays passing in its vicinity, and gives rise to spectacular optical illusions, called gravitational lensing. Interstellar is the first Hollywood movie to attempt depicting a black hole as it would actually be seen by an observer nearby.

For this, the team at Double Negative Visual Effects, in collaboration with Kip Thorne, developed a numerical code to solve the equations of light-ray propagation in the curved spacetime of a Kerr black hole. It allows to describe gravitational lensing of distant stars as viewed by a camera near the event horizon, as well as the images of a gazeous acccretion disk orbiting around the black hole. For the gravitational lensing of background stars, the best simulations ever done are due to Alain Riazuelo[i], at the Institut d’Astrophysique in Paris, who calculated the silhouette of black holes that spin very fast, like Gargantua, in front of a celestial background comprising several thousands of stars.

BH_LMC_APOD-BR
Gravitational lensing produced by a black hole in a direction almost centered on the Large Magellanic Cloud. Above it one easily notices the southernmost part of the Milky Way with, from left to right, Alpha and Beta Centauri, the Southern Cross. The brightest star, close to the LMC is Canopus (seen twice). The second brightest star is Achernar, also seen twice. © Alain Riazuelo, CNRS/IAP

But perhaps the most striking image of the film Interstellar is the one showing a glowing accretion disk which spreads above, below and in front of Gargantua. Accretion disks have been detected in some double-star systems that emit X-ray radiation (with black holes of a few solar masses) and in the centers of numerous galaxies (with black holes whose mass adds up to between one million and several billion solar masses). Due to the lack of spatial resolution (black holes are very far away), no detailed image has yet been taken of an accretion disk ; but the hope of imaging accretion disks around black holes telescopically, using very long baseline interferometry, is nearing reality today via the Event Horizon Telescope[ii]. In the meanwhile, we can use the computer to reconstruct how a black hole surrounded by a disk of gas would look. The images must experience extraordinary optical deformations, due to the deflection of light rays produced by the strong curvature of the space-time in the vicinity of the black hole. General relativity allows the calculation of such an effect. Continue reading →