Sequel of the preceding post The Warped Science of Interstellar (3/6)

In november  2014, the Hollywood blockbuster and science-fiction movie Interstellar was released on screens and  much mediatic excitation arose about it.
This is the fourth of a series of 6 posts devoted to the analysis of some of the scientific aspects of the film, adapted from a paper I published last spring in Inference : International Review of Science.

A HUGE TIME DILATION

The elasticity of time is a major consequence of relativity theory, according to which time runs differently for two observers with a relative acceleration – or, from the Equivalence Principle, moving in gravitational fields of different intensities. This well-known phenomenon, checked experimentally to high accuracy, is called « time dilation ».

Thus, close to the event horizon of a black hole, where the gravitational field is huge, time dilation is also huge, because the clocks will be strongly slowed down compared to farther clocks. This is one of the most stunning elements of the scenario of Interstellar : on the water planet so close to Gargantua, it is claimed that 1 hour in the planet’s reference frame corresponds to 7 years in an observer’s reference frame far from the black hole (for instance on Earth). This corresponds to a time dilation factor of 60,000. Although the time dilation tends to infinity when a clock tends to the event horizon (this is precisely why no signal can leave it to reach any external observer), at first sight a time dilation as large as 60,000 seems impossible for a planet orbiting the black hole on a stable orbit.

As explained by Thorne in his popular book, such a large time dilation was a « non-negotiable » request of the film director, for the needs of the story. Intuitively, even an expert in general relativity would estimate impossible to reconcile an enormous time differential with a planet skimming up the event horizon and safely enduring the correspondingly enormous gravitational forces. However Thorne did a few hours of calculations and came to the conclusion that in fact it was marginally possible (although very unlikely). The key point is the black hole’s spin. A rotating black hole, described by the Kerr metric, behaves rather differently from a static one, described by the Schwarzschild metric. The time dilation equation derived from the Kerr metric takes the form:

1 – (dτ/dt)² = 2GMr/c²rho², where rho² = r² + (J/Mc)²cos²θ.

Substituting for dτ = 1 hour and dt = 7 years, one obtains the following relation:

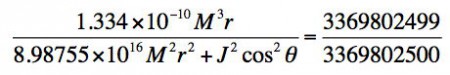
This equation fully describes a black hole of mass M, rotating with angular momentum J, as observed by an observer at radial coordinate r and angular coordinate θ. The fraction on the right-hand-side fully depicts the 1 hour = 7 years dilation effect. For the Schwarzschild metric, the orbital radius should be no smaller than 3 times the gravitational radius, and such a time dilation could not be achieved for the planet of the film. But as already said, the Kerr metric allows for stable orbits much closer to the event horizon. Calculations indicate that for M = 10⁸ solar masses, we get r = 1.48×10¹³ cm, θ = π and J = 8.80275×10⁵⁷ J.s. This implies a black hole angular momentum J extraordinarily close (at 10^-10) to the maximal possible value J_max, a circular orbit lying in the equatorial plane and a radius orbit practically equal to the black hole’s gravitational radius. All this is theoretically possible, but by no ways realistic.

A CLEVER USE OF THE PENROSE PROCESS

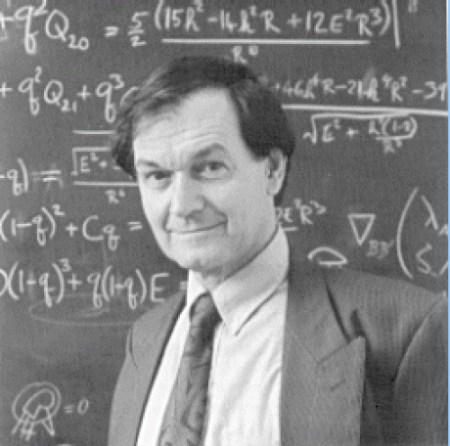
Another effect specific to the physics of rotating black holes, which was correctly depicted in Interstellar, is the Penrose process. The astronauts use it to benefit of a particularly efficient gravitational assistance (called « slingshot effect »), which allows their spaceship to plunge very close to the event horizon and escape with an increased energy. In effect, the laws of Kerr black hole physics say that, although a black hole prevents any radiation or matter from escaping, it can give up a part of its rotational energy to the external medium.

The key role is played by the ergosphere, a region between the event horizon and the static limit below which, like in a maelstrom, space-time itself is irresistibly dragged along with it (the so-called « Lense-Thirring effect »). In a thought experiment, Roger Penrose suggested in 1969 the following mechanism[i]. A projectile disintegrates into the ergosphere, one of the fragments falls into the event horizon in a direction opposite to the black hole’s rotation, while the other fragment can leave and be recovered, carrying more energy than the initial projectile. Replace the projectiles by a spaceship which leaves a part of it to fall into the black hole along a carefully chosen retrograde orbit, and le tour est joué.

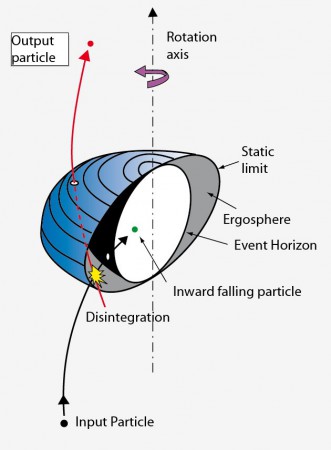
The calculations indicate that one can extract an energy equivalent to the rest-mass energy of the part lost into the black hole, which, according to the famous formula E=mc² can already be huge, plus an additional energy extracted from the spinning black hole, which has been slowed down by the infalling fragment in a retrograde orbit. For a black hole like Gargantua, rotating at almost the maximal speed, repeated Penrose processes could extract 29% of its mass.

Go to next post The Warped Science of Interstellar (5/6)

REFERENCES

[i] Penrose, R. : Gravitational Collapse: the Role of General Relativity, Rivista del Nuovo Cimento, Numero Speziale 1, 252 (1969).