In view of the total solar eclipse of 2017 Aug 21 through the United States, this is a reminder of the role of solar eclipses in the developments of astronomy and astrophysics.
It is taken from a chapter of my book Glorious Eclipses, presented elsewhere in this blog.
Summary
Eclipses of the Sun and Moon have never ceased to provide us with a host of lessons about the nature of the universe around us. The first of these lessons concerned the celestial bodies directly involved in eclipses: namely the Earth, Moon, and Sun. Indeed, back in antiquity, the proof that the Earth was round, and the first measurements of the respective sizes and distances of the Moon and Sun were deduced from the observation of eclipses. In the 19th century, it was the normally invisible atmosphere of the Sun that was revealed thanks to eclipses. Far from being the perfectly round, and sharply defined ball of hot gas that it appears to the eye – appropriately protected by suitable filters, of course – the Sun is found to be a sprawling giant, overflowing with energy, plasma, and particles, that extends its influence throughout the whole Solar System. Eclipses also provoked the discovery of helium, the second most abundant element in the Sun, and in the universe as a whole. In a more surprising manner, in the 20th century, Einstein’s General Relativity, a fundamental theory about space, was tested experimentally for the first time, thanks to an eclipse. It is on this new vision of the universe, which explains gravitation in terms of the ‘curvature of space-time’, that all our current knowledge of the origin, the structure, and the evolution of the universe, depends, by way of the fascinating concepts of an expanding universe, the Big Bang, and black holes.

The Earth is round

The first demonstration of an astrophysical nature resulting from eclipses is the one given by Aristotle concerning the fact that the Earth is round. The astronomical views of this Greek philosopher are well-known to us, thanks to his two works, known to us as Meteorology and On the Heavens, dating from the 4th century BC. Like other thinkers of his day, Aristotle believed that all heavenly bodies were spherical, because to him heavenly bodies were a reflection of divine perfection, and the sphere is the most outstandingly perfect geometrical figure. But this argument was not a physical demonstration, because, naturally, Aristotle did not have any experimental means of confirming the spherical nature of the planets and stars.
As far as the Moon was concerned, the philosopher adopted an explanation attributed to the Pythagoreans, namely that the observed appearance of the Moon throughout its various phases corresponded to a spherical body, half of which is illuminated by the Sun. As for the spherical nature of the Earth, the proof given by Aristotle is quite original: he notes that an eclipse of the Moon is caused by the shadow of the Earth, and that the circular shape to the edge of the shadow seen on the Moon’s surface implies that our world is spherical
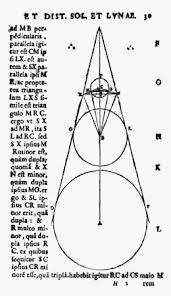
Sizes and distances of the Moon and Sun
The golden age of Greek astronomy flourished at Alexandria. Since its foundation under the reign of Ptolemy Soter (3rd century BC), the Alexandrian school brought together brilliant mathematicians and geometers, such as Euclid, Archimedes, and Apollonius. Similarly, the greatest ancient astronomers Aristachus of Samos, Eratosthenes, and Hipparchus, as well as Ptolemy (2nd century BC), all worked there.
Aristarchus (310-230 BC) is nowadays known for having been the first to voice the heliocentric theory, i.e., that it is the Sun that reigns at the centre of the world system, not the Earth as was believed at the time. His statement does not appear in any known work, but it was reported by Archimedes and by Plutarch. The only work of Aristarchus that has come down to us relates to the sizes and distances of the Sun and the Moon.
The Alexandrian astronomer completely reopened this question, which had been discussed since the 4th century BC. The Pythagoreans had positioned the heights of the celestial bodies according to musical intervals. Eudoxus, the brilliant disciple of Plato, had estimated the diameter of the Sun as nine times that of the Moon. As for Aristarchus, he devised an ingenious geometrical method of calculating the distance ratios of the Sun and Moon.
He found that the Sun lay at a distance between 18 and 20 times that of the Moon. (In fact, it is 400 times as far.) By an argument based on the observation of eclipses, he determined the diameter of the Moon as one third of that of the Earth, which is very close to the actual value. He also announced that the diameter of the Sun is seven times that of the Earth. Even though Aristarchus considerably underestimated the size of the Sun, because it is actually 109 times as large as the Earth, he had grasped the essential fact that the daytime star was much larger than the Earth. It was precisely this result that led him to the heliocentric hypothesis. He did, in fact, argue that under these circumstances, it was logical to believe that the Earth and the other celestial bodies revolved around the Sun, rather than the reverse. Aristachus was before his time. The world had to wait until 1543 and the work by Copernicus, before the heliocentric theory was again put forward, this time with success.
A century after Aristachus, and again at Alexandria, Hipparchus developed a complete theory of the Moon. He defined the lengths of the synodic month (or lunation, the period in which the Moon returns to the same position relative to the Sun); the draconitic month (the period for the Moon to return to the same position relative to the nodes of its orbit); and the anomalistic month (the period for the Moon to return to perigee or apogee). The immense improvements that Hipparchus brought to theories of the apparent motion of the Moon and Sun enabled him to have far more success than his predecessors in dealing with the problem of predicting eclipses, which had always been of immense interest.
Hipparchus considerably extended Aristarchus’ method: by observing the angular diameter of the shadow of the Earth at the Moon’s distance during a lunar eclipse, and comparing it with the known apparent diameters of the Sun and Moon (about half a degree), he obtained the ratio of the Earth-Moon and Earth-Sun distances, giving one when the other is known. Pappus, another famous astronomer of the Alexandrian school, recounts that Hipparchus made the following observation of: “An eclipse of the Sun, which in the area of the Hellespont was precisely an exact eclipse of the whole Sun; such that none of it was visible, but at Alexandria, in Egypt, about 4/5 of its diameter were hidden. By means of the foregoing arguments, [Hipparchus] showed that, measured in units where the radius of the Earth has the value of 1, the smallest distance to the Moon is 71, and the larger 83. Whence the average of 77.“
The total solar eclipse mentioned is that of 20 November 129 BC. The actual value of the Earth-Moon distance is 60,4 terrestrial radii.

The empire of the Sun
Continue reading TOTAL SOLAR ECLIPSE 2017 : THE ROLE OF SOLAR ECLIPSES IN ASTROPHYSICS