Sequel of the preceding post A Brief History of Space (3/4) : From Descartes to Schwarzschild

Cosmology developed rapidly after the completion of general relativity by Albert Einstein, in 1915. In this theory, the Universe does not reduce to a space and a time which are absolute and separate; it is made up of the union of space and time into a four dimensional geometry, which is curved by the presence of matter.

It is in fact the curvature of space-time as a whole which allows one to correctly model gravity, and not only the curvature of space, such as Clifford had hoped. The non-Euclidean character of the Universe appeared from then on not as a strangeness, but on the contrary as a physical necessity for taking account of gravitational effects. The curvature is connected to the density of matter. In 1917, Einstein presented the first relativistic model for the universe. Like Riemann, he wanted a closed universe (one whose volume and circumference were perfectly finite and measurable) without a boundary; he also chose the hypersphere to model the spatial part of the Universe.

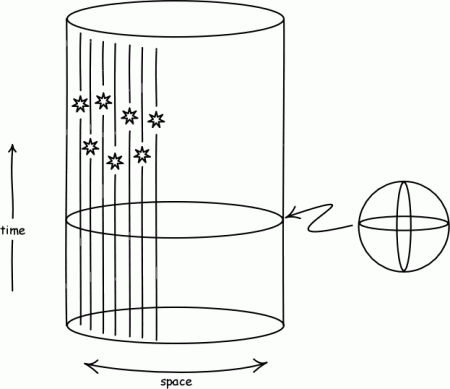
At any rate, Einstein’s model made the hypothesis of a static Universe, with the radius of the hypersphere remaining invariable over the course of time. In truth, the cosmological solutions of relativity allow complete freedom for one to imagine a space which expands or contracts over the course of time: this was demonstrated by the Russian theorist Alexander Friedmann, between 1922 and 1924.

At the same time, the installment of the large telescope at Mount Wilson, in the United States, allowed for a radical change in the cosmic landscape. In 1924, the observations of Edwin Hubble proved that the nebula NGC 6822 was situated far beyond our galaxy. Very rapidly, Hubble and his collaborators showed that this was the case for all of the spiral nebulae, including our famous neighbor, the Andromeda nebula: these are galaxies in their own right, and the Universe is made up of the ensemble of these galaxies. The “island-universes” already envisaged by Thomas Wright, Kant and Johann Heinrich Lambert were legitimized by experiment, and the physical Universe seemed suddenly to be immensely enlarged, passing from a few thousand to several dozen million light-years at the minimum. Beyond this spatial enlargement, the second major discovery concerned the time evolution of the Universe. In 1925, indications accumulated which tended to lead one to believe that other galaxies were systematically moving away from ours, with speeds which were proportional to their distance.

This experimental result remained totally incomprehensible until the scientific community accepted, in the early 1930’s, the solution proposed in 1927 by the Belgian physicist Georges Lemaître: space as a whole dilates over the course of time; it is in expansion, and this expansion carries the ensemble of galaxies along with it.

The question of the finite or infinite nature of space can be perfectly well posed in the framework of the solutions of Friedmann and Lemaître. These cosmological models assume that irregularities in the distribution of matter are negligible, as a consequence of which the Universe has everywhere the same geometric properties. These properties are of only two types: the curvature, constant in space but whose sign remains to be determined, and the topology.

As far as the curvature is concerned, three families of space were considered: Euclidean space (with zero curvature), spherical space (with positive curvature) and Lobachevskian space (also called hyperbolic space, with negative curvature). Spherical space, as a rule, is of finite volume. This is the basic reason why the pioneers of relativistic cosmology – Einstein, de Sitter, Friedmann, and Lemaître – chose it as the starting point.

General relativity shows how to indirectly measure the curvature of space. Its value depends on the average density of matter and energy that it contains. If the real density passes a critical threshold, the curvature is positive and space is finite. For sixty years, observational cosmology has sought to determine the curvature of space by taking a census of all the forms of energy and matter that contribute to it.

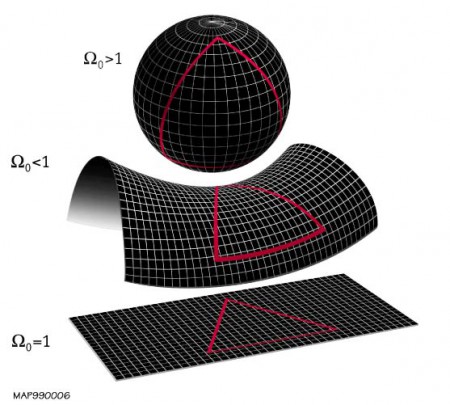
However, for the geometries of the two other families, Euclidean and hyperbolic, the finite or infinite character of space no longer depends simply on the curvature and on the energy density: it depends on the topology. There is presently no general physical theory which allows one to predict the global topology of the Universe starting from its local characteristics.