One year ago exactly, in november 2014, the Hollywood blockbuster and science-fiction movie Interstellar was released on screens and much mediatic excitation arose about it.
This is the first of a series of 6 posts devoted to the analysis of some of the scientific aspects of the film, adapted from a paper I published last spring in Inference : International Review of Science.
 Interstellar tells the adventures of a group of explorers who use a wormhole to cross intergalactic distances and find potentially habitable exoplanets to colonize. Interstellar is a fiction, obeying its own rules of artistic license : the film director Christopher Nolan and the screenwriter, his brother Jonah, did not intended to put on the screens a documentary on astrophysics – they rather wanted to produce a blockbuster, and they succeeded pretty well on this point. However, for the scientific part, they have collaborated with the physicist Kip Thorne, a world-known specialist in general relativity and black hole theory. With such an advisor, the promotion of the movie insisted a lot on the scientific realism of the story, in particular on black hole images calculated by Kip Thorne and the team of visual effects company Double Negative. The movie also refers to many aspects of contemporary science, going from well-studied issues such as warped space, fast-spinning black holes, accretion disks, tidal effects or time dilation, to much more speculative ideas which stem beyond the frontiers of our present knowledge, such as wormholes, time travel to the past, extra-space dimensions or the « ultimate equation » of an expected « Theory of Everything ».
Interstellar tells the adventures of a group of explorers who use a wormhole to cross intergalactic distances and find potentially habitable exoplanets to colonize. Interstellar is a fiction, obeying its own rules of artistic license : the film director Christopher Nolan and the screenwriter, his brother Jonah, did not intended to put on the screens a documentary on astrophysics – they rather wanted to produce a blockbuster, and they succeeded pretty well on this point. However, for the scientific part, they have collaborated with the physicist Kip Thorne, a world-known specialist in general relativity and black hole theory. With such an advisor, the promotion of the movie insisted a lot on the scientific realism of the story, in particular on black hole images calculated by Kip Thorne and the team of visual effects company Double Negative. The movie also refers to many aspects of contemporary science, going from well-studied issues such as warped space, fast-spinning black holes, accretion disks, tidal effects or time dilation, to much more speculative ideas which stem beyond the frontiers of our present knowledge, such as wormholes, time travel to the past, extra-space dimensions or the « ultimate equation » of an expected « Theory of Everything ».
It is the reason why, beyond the subjective appreciations that everyone may have about the fiction story itself, many people – physicists and science journalists – have taken the internet to write articles lauding or criticizing the science shown in the movie. Kip Thorne has written a popular book, The Science of Interstellar [i], to explain how he tried to respect scientific accuracy, despite the sometimes exotic demands of Christopher and Jonah Nolan, ensuring in particular that the depictions of black holes and relativistic effects were as accurate as possible.
The aim of this article is not to write a (inevitably subjective) review of Interstellar as a fiction story, but to decipher some of the scientific notions, which support the framework of the movie.
AN ARTIFICIAL WORMHOLE IN THE SOLAR SYTEM ?
In the first part of the film, we are told that a « gravitational anomaly », called a wormhole, has been discovered out near Saturn several decades ago, that a dozen habitable planets have been detected on the « other side » and a dozen astronauts sent to explore them. In particular, one system has three potentially habitable planets, and it is now the mission of the hero, Cooper, to pilot a spaceship through the wormhole and find which planet is more suitable for providing humanity a new home off the dying Earth.
Wormholes arise as mathematical, idealized solutions of the equations of general relativity that describe the shape of space-time generated by a black hole. Their description can be made pictorial by a technique called embedding. As the name suggests, the game is to visualize the shape of a given space by embedding it in a space with an additional dimension. The mapping is useless for the full 4-dimensional space-time of general relativity, as it would have to be embedded in a 5-dimensional space, which is impossible to visualize. But in the case of a non-rotating black hole, the space-time geometry, described by the Schwarzschild metric, remains fixed at all times ; furthermore, due to spherical symmetry, no information is lost by looking only at equatorial slices passing through the center of the sphere. It then becomes easy to visualize all the details of the curvature of the Schwarzschild geometry as a 2-dimensional surface embedded in the usual 3-dimensional Euclidean space. The result comes to a surprise : the embedding surface consists of a paraboloid-shaped throat linking two distinct sheets of space-time. Ludwig Flamm discovered the paraboloid shape as soon as 1916, and Albert Einstein and Nathan Rosen[ii] first studied the Schwarzschild throat in 1935. It has a minimum radius equal to the Schwarzschild radius r =2GM/c2, where M is the mass of the black hole, G the gravitational constant and c the speed of light : it corresponds to the event horizon – the immaterial frontier of the black hole – reduced to a circle. For a typical stellar black hole with M = 10 solar masses, we get r = 30 km. It is the size assumed in Interstellar.
The Schwarzschild throat (also called the Einstein-Rosen bridge) joins the upper and lower sheets which are perfectly symmetrical, and which we are at liberty to interpret as « parallel universes ». In other words, the throat appears to the upper universe like a black hole consuming matter, light and energy, but for the lower universe it appears as a « white fountain » expelling matter, light and energy.

Now, general relativity determines only the local curvature of the space-time, and not its global shape. In particular, it allows the two distinct sheets to be different regions of the same universe. We have now a black hole and a white fountain in the same space-time at an arbitrary distance from each other, but linked by a stretched-out throat, baptized wormhole by John Wheeler in 1957 (Wheeler also coined the term « black hole », but only ten years later). We can figure out a wormhole like a tunnel with two ends, each in separate points in space-time, and that tunnel would work as a shortcut to travel through space and time. For example, Charles Misner[iii] found a solution of the wormhole equations allowing to travel from the solar system to the nearest star, Proxima Centauri, located at 4.2 light-years, in a time shorter than 4.2 years, however without exceeding the speed of light.
Now, coming back to the Interstellar story, two major problems arise. First, there is no wormhole without a black hole. Second, is a wormhole traversable, and can it be really used by a spaceship to travel in space-time ?
For the first one, there are clearly several scientific caveats in the scenario. The most common black holes are formed by the gravitational collapse of massive stars, and consequently have a few solar masses. According to the Schwarzschild formula given above, their radius, and consequently that of their putative wormhole, is of order of a few kilometers only, and the tidal forces they generate (see below) are so huge that any spaceship or astronaut would be torn apart at a distance of several thousands kilometers, i.e. well before being able to reach the event horizon and penetrate it. Besides, since about one star over 10,000 is massive enough to generate a black hole, the latter are pretty rare : it is estimated that the average density of stellar mass black holes in our region of the Milky Way is of the order of 0.00001 per cubic light year. It would thus be extraordinarily improbable that a stellar black hole is so close to us. And even if it were so, at the distance of Saturn, its huge gravitational field would completely destroy the stability of our solar system ! It is the reason why the Nolan’s brothers have taken a pure science-fiction option : the wormhole near Saturn has been artificially created by a very advanced civilization, and placed there to help humanity escape the solar system (at the end of the movie, we understand that these aliens were in fact advanced humans from the future ; they created the black hole and its associated wormhole in the first place, manipulating time and events so that things had to unfold the way they did).

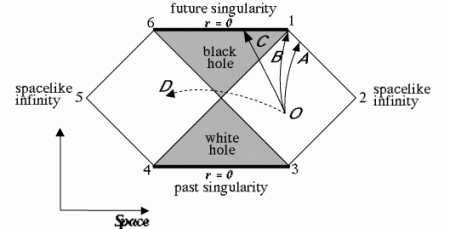
The second problem is the traversability of wormholes. The calculations for a non-rotating black hole, described by the Schwarzschild geometry, show that the wormhole is « strangled in the middle » by the infinite gravitational field of a singularity located at the center r=0, so that nothing can pass through it.
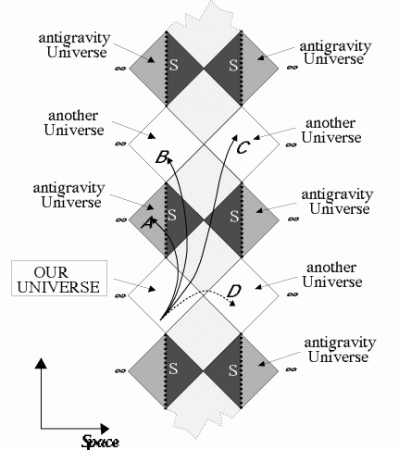
However, natural black holes, like stars, must be rotating, and it that case the geometry is much more subtle and complex than the Schwarzschild one. It is described by the Kerr metric (as discovered in 1962 by the new Zealand physicist Roy Kerr). And in that case, the mapping technique described above for the Schwarzschild geometry gives a much more complicated and interesting space-time structure, investigated in the 1960’s by Brandon Carter (my former PhD advisor) and Roger Penrose[iv]. First of all, the central singularity is no more reduced to a central point at r=0, but has the shape of a ring lying in the equatorial plane of the rotating black hole. As a consequence, the ring no more defines an edge of the space-time geometry, because a traveller, apart from the dangers of tidal forces, could come safely within a hair’s breadth of the annular singularity provided he does not touch it, or he can even pass through it. The Penrose-Carter diagrams suggest fascinating possibilities for exploration (see e.g. Luminet[v]). Allowable trajectories show that it is theoretically possible to penetrate the interior of a rotating black hole – preferably a very large one, so that the spaceship is not destroyed by tidal forces -, fly above the plane of the singular ring, and escape the black hole by emerging into an exterior universe (which could be topologically the same as the starting one). Along other trajectories, it could also go to the « other side » of the singularity by passing through the ring, and emerge into a completely unknown universe. In such cases, Kerr black holes would have open wormholes, offering fantastic possibilities for space-time travel !
Alas, the Penrose-Carter diagrams are idealized representations of the space-time structure. In the real universe, astrophysical black holes, rotating or not, are formed by physical processes such as gravitational collapse, and in that case, all the general relativistic calculations say that wormholes are unstable : as soon as they are formed, they would also gravitationally collapse and would be not traversable. But this is not quite the end of the story : come into play general relativistic calculations involving also quantum processes. A possible escape has been proposed in 1988 by Thorne and his students[vi] : wormholes that are laced with matter or energy exerting an enormous « negative pressure » (i. e. a repulsive tension) could be stable and traversable. Such forms of matter or energy are called « exotic ». It happens that, in the framework of quantum mechanics, some energy states of the quantum vacuum obtained by the so-called Casimir effect have the required properties to produce exotic energy. Of course, all of this is highly speculative, but not theoretically impossible – even if the amount of negative energy required maintaining the wormhole open would be greater than the total energy emitted by the Sun during one full year…
Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity[vii]. Thus, for a Hollywood sci-fi movie, the screenwriters felt free to imagine that a very advanced civilization could construct a negative wormhole – perhaps by growing a microscopic negative one, as permitted by quantum mechanics –, and use it effectively as a space-time shortcut.
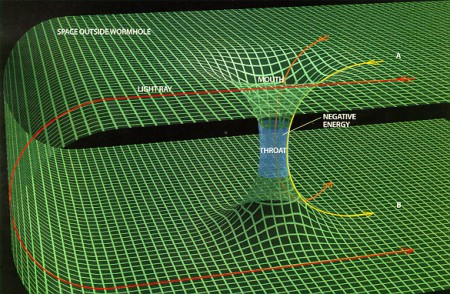
 Even allowing this fantastic idea, there is nothing telling us that a spaceship (and the humans inside), made of normal matter, could cross the negative energy region safely. Nevertheless, the theoretical possibility enabled the popular American astronomer-writer Carl Sagan to construct his novel Contact (1985) using the idea of communication with extra-terrestrial civilizations by means of wormholes, and already at the time it was Kip Torne who advised Sagan on the possibilities of wormholes.
Even allowing this fantastic idea, there is nothing telling us that a spaceship (and the humans inside), made of normal matter, could cross the negative energy region safely. Nevertheless, the theoretical possibility enabled the popular American astronomer-writer Carl Sagan to construct his novel Contact (1985) using the idea of communication with extra-terrestrial civilizations by means of wormholes, and already at the time it was Kip Torne who advised Sagan on the possibilities of wormholes.
For Interstellar, Thorne went beyond and, just to help the team of visual effects, tried to calculate what would give a journey through an artificially created wormhole. Except for the spherical shape of the wormhole, which can be appreciated by the spectators when the spaceship approaches, most of the scientific calculations were not retained by the filmmakers, because of the strange effects generated, arguably non understandable for a general audience. For the rest, we can be sure that, with our present-day knowledge, a traversable wormhole is not only very improbable, but if it existed, its crossing would not at all look like it is shown in the movie !

To conclude this section, it is to be noticed that scientific visualizations of traversable wormholes had already been calculated in 2006 by Alain Riazuelo at the Institut d’Astrophysique de Paris, and the result, available on DVD[viii], is much more spectacular than the artistic rendering shown in Interstellar.
Go to the next post The Warped Science of Interstellar (2/6)
REFERENCES
[i] K. Thorne : The Science of Interstellar, Norton & Company (november 2014).
[ii] A. Einstein, N. Rosen :The Particle Problem in the General Theory of Relativity, Physical Review 48: 73 (1935).
[iii] C. W. Misner : Wormhole Initial Conditions, Physical Review 118, 1110 (1960).
[iv] B. and C. DeWitt (eds) : Black Holes (Les Houches School 1972), Gordon Breach, New York (1973)
[v] J.-P. Luminet : Black Holes, Cambrige University Press, chap. 12. For the French readers, the updated version is J.-P. Luminet : Le destin de l’univers, trous noirs et énergie sombre, Paris : Fayard (2006).
[vi] M. Morris, M. S., Thorne, K. S., and Yurtsever, U. : Wormholes, Time Machines and the Weak Energy Condition, Phys. Rev. Letters, 61, 1446-1449 (1988).
[vii] M. Visser : Lorentzian Wormholes, American Institute of Physics, 1996.
[viii] A. Riazuelo : Voyage au cœur d’un trou noir, DVD (Paris : Sciences et Avenir), 2008.


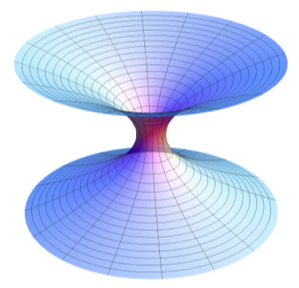
Is there a English translated or captioned version of Voyage au cœur d’un trou noir? I would love to hear what they’re saying in the video. Otherwise, I’ll just have to use the auto-captioning from YouTube.
For an English comment you can look at the video https://www.youtube.com/watch?v=5Oqop50ltrM