La conjecture de Riemann résiste depuis plus de 150 ans aux efforts des mathématiciens les plus imaginatifs. Riemann l’a énoncée en 1859 mais l’a laissée pour ainsi dire en plan avant de passer à la suite de ce qui le préoccupait sur l’instant. L’importance de cette conjecture réside dans le fait qu’elle est au cœur de la problématique concernant la recherche de la répartition si mystérieuse des nombres premiers. De surcroît, bien des théorèmes de la Théorie des nombres reposent sur elle, et s’en trouveraient ipso facto démontrés si elle l’était enfin. A n’en pas douter, cette conjecture, une fois prouvée, figurerait dans la liste des théorèmes utiles au sens défini par Jean Dieudonné (ne pas oublier le prénom !) dans son très beau livre “Pour l’honneur de l’esprit humain” (Hachette, 1981), ce que confirme le fait qu’elle figure dans la fameuse liste de problèmes dressée par Hilbert en 1900, et qu’elle est aussi l’un des sept problèmes du Prix du millénaire selon le Clay Mathematical Institute.

Ce qu’a affirmé Riemann concerne l’illustre fonction portant son nom, dont il prétend que les zéros , autres que les entiers pairs négatifs, sont tous sur une droite du plan complexe située à la droite de l’axe imaginaire, à la distance  de celui-ci. Depuis Riemann, des résultats importants ont été établis ; par exemple, Hardy a démontré en 1914 que la fameuse droite (dite ligne critique) contient une infinité de zéros, mais cela ne veut pas dire qu’ils y sont tous…

Il est intéressant de constater que les tentatives de preuve ne sont pas l’apanage des mathématiciens : nombre de physiciens s’y sont essayés sans y parvenir non plus malgré des approches sensiblement différentes comme par exemple la recherche d’opérateurs hermitiques dont le spectre serait précisément constitué par tous les nombres …

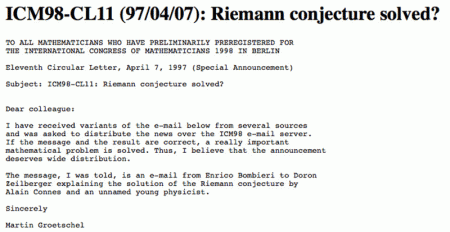
Le mathématicien britannique Matthew R. Watkins a constitué un site rassemblant notamment diverses fausses preuves récentes de cette conjecture, intitulé “Proposed (dis)proofs of the Riemann Hypothesis”, auquel le lecteur curieux est renvoyé. Il pourra notamment y découvrir la fameuse farce de Bombieri, un certain 1er avril (voir figure)…

Sur ces questions, graves, profondes et parfois anecdotiques, on se doit de citer le très beau livre de Marcus du Sautoy La symphonie des nombres premiers (Collection Points – Science, Seuil 2007), dont la lecture est un voyage passionnant dans un univers à la portée de tous.